Równania

Właściciel sklepu sportowego kupił w hurtowni deskorolki i kaski. Cena hurtowa deskorolki była o 60 zł wyższa niż cena hurtowa kasku. Właściciel sklepu ustalił cenę sprzedaży deskorolki o 20% wyższą od ceny hurtowej, a cenę sprzedaży kasku – o 40% wyższą od ceny hurtowej. Deskorolka i kask łącznie kosztowały w sklepie 397 zł. Oblicz łączny koszt zakupu po cenach hurtowych jednej deskorolki i jednego kasku. Zapisz obliczenia.

Grupa turystów w ciągu pierwszej godziny marszu pokonała pewien odcinek trasy. W każdej następnej godzinie pokonywany dystans był o 0,5 km krótszy od dystansu pokonanego w poprzedniej godzinie. W ciągu pierwszych pięciu godzin marszu turyści przeszli łącznie 17,5 km trasy.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Odcinek trasy, który turyści przeszli w pierwszej godzinie marszu, miał długość

W pewnym zakładzie każdy z pracowników codziennie maluje taką samą liczbę jednakowych ozdób. Pracownicy potrzebowali 12 dni roboczych, aby wykonać zamówienie. Gdyby było ich o dwóch więcej, to czas wykonania tego zamówienia byłby o 3 dni krótszy.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Liczbę pracowników x tego zakładu można obliczyć, rozwiązując równanie

Na rysunku przedstawiono prostokąt, którego wymiary są opisane za pomocą wyrażeń.

W zawodach sportowych każdy zawodnik miał pokonać trasę składającą się z trzech części. Pierwszą część trasy zawodnik przejechał na rowerze, drugą część − prowadzącą przez jezioro − przepłynął, a trzecią – przebiegł. Na rysunku przedstawiono schemat tej trasy.

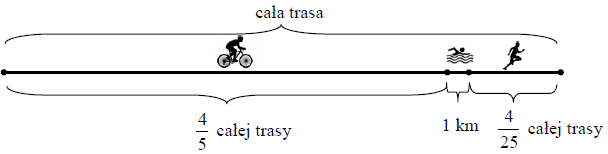
Na podstawie informacji wybierz zdanie prawdziwe.

A. Cała trasa miała długość 50 km.
B. Zawodnik przebiegł 8 km.
C. Odległość, którą zawodnik przebiegł, była o 4 km większa od odległości, którą przepłynął.
D. Odległość, którą zawodnik przejechał na rowerze, była 5 razy większa od odległości, którą przebiegł.

W pewnej klasie liczba chłopców stanowi 80% liczby dziewcząt. Gdyby do tej klasy doszło jeszcze trzech chłopców, to liczba chłopców byłaby równa liczbie dziewcząt. Ile dziewcząt jest w tej klasie? Zapisz obliczenia.

Jeden z kątów wewnętrznych trójkąta ma miarę α, drugi ma miarę o 30° większą niż kąt α, a trzeci ma miarę trzy razy większą niż kąt α.

Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.

Trójkąt ten jest

A. równoboczny.
B. równoramienny.
C. rozwartokątny.
D. prostokątny.

Obwód trapezu równoramiennego jest równy 72 cm, ramię ma długość 20 cm, a różnica długości podstaw wynosi 24 cm. Oblicz pole tego trapezu. Zapisz obliczenia.

Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.

Połowa uczestników wycieczki urodziła się w Polsce, co trzeci urodził się w Niemczech, a pięciu pozostałych we Francji. W wycieczce brało udział

A. 26 osób.   B. 30 osób.   C. 46 osób.   D. 60 osób.

Hania, płacąc w sklepie za trzy tabliczki czekolady, podała kasjerce 15 zł i otrzymała 0,60 zł reszty. Które z równań odpowiada treści zadania, jeśli cenę tabliczki czekolady oznaczymy przez x?

A. 3x + 0,6 = 15   B. 3x + 15 = 0,6   C. 0,6x + 3= 15   D. 15x + 0,6 = 3

Trzy lata temu posadzono przed domem krzew. Co roku podwajał on swoją wysokość i teraz ma 144 cm. Jeśli przez x oznaczymy wysokość krzewu w dniu posadzenia, to informacjom z zadania odpowiada równanie

A. x = 144   B. 4x = 144   C. 6x = 144   D. 8x = 144

Na rzece zbudowano most, który zachodzi na jej brzegi: 150 metrów mostu zachodzi na jeden brzeg, a ¹/₃ długości mostu na drugi. Oblicz szerokość rzeki, jeżeli stanowi ona ¹/₆ długości mostu. Zapisz obliczenia.

Podczas trzydniowej pieszej wycieczki uczniowie przeszli 39 km. Drugiego dnia pokonali dwa razy dłuższą trasę niż pierwszego dnia, a trzeciego o 5 km mniej niż pierwszego. Ile km przebyli pierwszego dnia?

A. 6   B. 11   C. 22   D. 28

W wycieczce rowerowej uczestniczy 32 uczniów. Chłopców jest o 8 więcej, niż dziewcząt. Ilu chłopców jest w tej grupie?

A. 12   B. 16   C. 20   D. 24

Jacek i Paweł zbierają znaczki. Jacek ma o 30 znaczków więcej niż Paweł. Razem mają 350 znaczków. Ile znaczków ma Paweł?

A. 145   B. 160   C. 190   D. 205

Paweł kupił australijski znaczek i 3 znaczki krajowe. Każdy znaczek krajowy kosztował tyle samo. Za wszystkie znaczki zapłacił 16 zł. Ile kosztował znaczek australijski, jeżeli był pięciokrotnie droższy niż znaczek krajowy?

A. 4 zł   B. 10 zł   C. 12 zł   D. 13 zł

Do pracowni komputerowej zakupiono 8 nowych monitorów i 6 drukarek za łączną kwotę 9400 zł. Drukarka była o 300 zł tańsza niż monitor. Cenę monitora można obliczyć, rozwiązując równanie:

A. 8x + 6(x + 300) = 9400
B. 8x + 6(x – 300) = 9400
C. 8(x-300) + 6x = 9400
D. 8(x + 300) + 6(x-300) = 9400

Marcin przebywa autobusem 3/4 drogi do jeziora, a pozostałą część piechotą. Oblicz odległość między domem Marcina, a jeziorem, jeżeli trasa, którą przebywa pieszo, jest o 8 km krótsza niż trasa, którą przebywa autobusem. Zapisz obliczenia.