Próbny egzamin ósmoklasisty Matematyka 2020 CKE
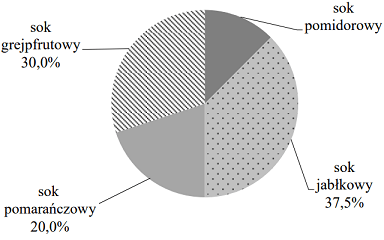
Na diagramie kołowym przedstawiono procentowy udział soków o różnych smakach, które zostały sprzedane podczas festynu. Najmniej sprzedano soku pomidorowego, tylko 15 kartonów, a najwięcej – soku jabłkowego.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
I. Sprzedano łącznie 125 kartonów soków. PRAWDA/FAŁSZ
II. Sprzedano o 30 kartonów więcej soku jabłkowego niż pomidorowego. PRAWDA/FAŁSZ
W liczbie pięciocyfrowej 258#4, podzielnej przez 4 i niepodzielnej przez 3, cyfrę dziesiątek zastąpiono znakiem „#”.
Jakiej cyfry na pewno nie zastąpiono znakiem „#”? Wybierz właściwą odpowiedź spośród podanych.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość wyrażenia \(\frac{4}{3}\cdot 3-{{2}^{3}}\) jest równa
Miejscowości A i B położone na przeciwległych brzegach jeziora są połączone dwiema drogami – drogą polną prowadzącą przez punkt P i drogą leśną prowadzącą przez punkt L. Długość drogi polnej APB wynosi 10 km, a długość drogi leśnej ALB jest równa 6 km.
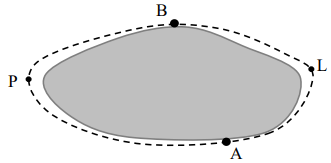
Matylda i Karol wyruszyli na rowerach z miejscowości A do miejscowości B o godzinie 10:00. Matylda jechała drogą leśną, a Karol – drogą polną. Średnia prędkość jazdy Matyldy wynosiła 15km/h, a średnia prędkość Karola była równa 20km/h.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
I. Do miejscowości B Karol przyjechał wcześniej niż Matylda. PRAWDA/FAŁSZ
II.Matylda przyjechała do miejscowości B o godzinie 10:24. PRAWDA/FAŁSZ
Na treningu odmierzano za pomocą aplikacji komputerowej 15-minutowe cykle ćwiczeń, które następowały bezpośrednio jeden po drugim. Ola zaczęła ćwiczyć, gdy pierwszy cykl trwał już 2 minuty, a skończyła, gdy do końca trzeciego cyklu zostało jeszcze 7 minut.
Ile łącznie minut Ola ćwiczyła na zajęciach?
Wybierz właściwą odpowiedź spośród podanych.
Oskar jest o 6 lat starszy od swoich braci bliźniaków. Obecnie Oskar i jego dwaj bracia mają razem 42 lata. Ile lat ma obecnie każdy z bliźniaków?
Wybierz właściwą odpowiedź spośród podanych.
Marta przygotowała dwa żetony takie, że suma liczb zapisanych na obu stronach każdego żetonu jest równa zero. Widok jednej ze stron tych żetonów przedstawiono poniżej.
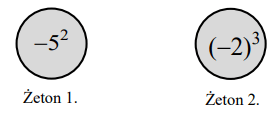
Jakie liczby znajdują się na niewidocznych stronach tych żetonów? Wybierz właściwą odpowiedź spośród podanych.
W układzie współrzędnych zaznaczono trójkąt ABC oraz punkt P należący do boku BC. Wszystkie współrzędne punktów A, B, C i P są liczbami całkowitymi.
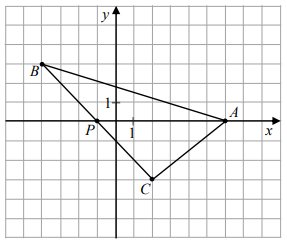
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
I. Pole trójkąta PAB jest równe polu trójkąta PAC. PRAWDA/FAŁSZ
II. Pole trójkąta ABC jest równe 21. PRAWDA/FAŁSZ
Trójkąt, w którym długości boków są do siebie w stosunku 3:4:5 nazywa się trójkątem egipskim.
Z odcinków o jakich długościach nie można zbudować trójkąta egipskiego? Wybierz właściwą odpowiedź spośród podanych.
Sprzedawca kupił od ogrodnika róże i tulipany za łączną kwotę 580 zł. Jeden tulipan
kosztował 1,20 zł, a cena jednej róży była równa 4 zł. Sprzedawca kupił o 50 tulipanów
więcej niż róż.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Jeśli liczbę zakupionych tulipanów oznaczymy przez t, to podane zależności opisuje równanie
Figura zacieniowana na rysunku jest równoległobokiem.
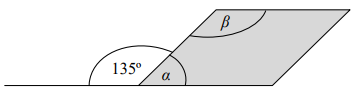
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
I. Suma miar kątów α i β wynosi 180°. PRAWDA/FAŁSZ
II. Kąt α ma miarę 3 razy mniejszą niż kąt β. PRAWDA/FAŁSZ
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Na rysunku przedstawiono trójkąt równoramienny KLM o ramionach KM i LM. Miara kąta KML jest dwa razy większa niż miara kąta KLM.
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
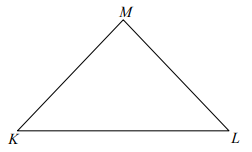
Miara kąta KLM jest równa A/B.
Trójkąt KLM jest C/D.
Małe trójkąty równoboczne o bokach długości 1 układano obok siebie tak, że uzyskiwano kolejne, coraz większe trójkąty równoboczne, według reguły przedstawionej na poniższym rysunku.
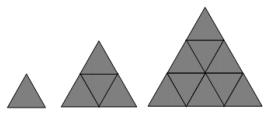
Ile małych trójkątów równobocznych należy użyć, aby ułożyć trójkąt równoboczny o podstawie równej 5? Wybierz właściwą odpowiedź spośród podanych.
W okręgu o środku S i promieniu 5cm narysowano cięciwę AB o długości 8cm.
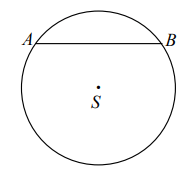
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
I. Odległość punktu S od cięciwy AB jest równa 3 cm. PRAWDA/FAŁSZ
II. Obwód trójkąta ASB jest równy 16 cm. PRAWDA/FAŁSZ
Średnia arytmetyczna dwóch ocen Janka z matematyki jest równa 3,5. Jaką trzecią ocenę musi uzyskać Janek, by średnia jego ocen była równa 4? Wybierz właściwą odpowiedź spośród podanych.
W tabeli podano cenniki dwóch korporacji taksówkowych. Należność za przejazd składa się z jednorazowej opłaty początkowej i doliczonej do niej opłaty zależnej od długości przejechanej trasy.
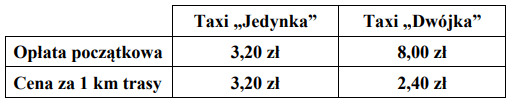
Pan Jan korzystał z Taxi „Jedynka”, a pan Wojciech – z Taxi „Dwójka”. Obaj panowie pokonali trasę o tej samej długości i zapłacili tyle samo. Ile kilometrów miała trasa, którą przejechał każdy z nich? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Zmieszano 40 dag rodzynek w cenie 12 zł za kilogram oraz 60 dag pestek dyni w cenie 17 zł za kilogram. Ile kosztuje 1 kilogram tej mieszanki? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Długości boków czworokąta opisano za pomocą wyrażeń algebraicznych, tak jak pokazano na rysunku.
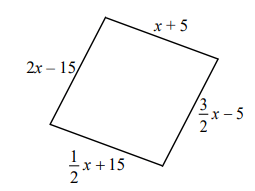
Uzasadnij, że jeśli obwód tego czworokąta jest równy 100 cm, to jest on rombem. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Pan Kazimierz przejechał trasę o długości 90 km w czasie 1,5 godziny. W drodze powrotnej tę samą trasę pokonał w czasie o 15 minut krótszym. O ile kilometrów na godzinę była większa jego średnia prędkość jazdy w drodze powrotnej? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Trapez równoramienny ABCD, którego pole jest równe 72cm2, podzielono na trójkąt AED i trapez EBCD. Odcinek AE ma długość równą 4 cm, a odcinek CD jest od niego 2 razy dłuższy. Oblicz pole trójkąta AED. Zapisz obliczenia.
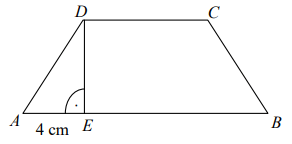 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Pudełko w kształcie prostopadłościanu o wymiarach przedstawionych na rysunku zawiera 32 czekoladki. Każda czekoladka ma kształt prostopadłościanu o wymiarach 2 cm, 2 cm i 1,5 cm. Ile procent objętości pudełka stanowi objętość wszystkich czekoladek? Zapisz obliczenia.
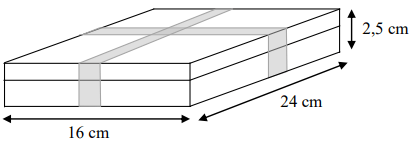 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.