Powtórka 8-kl. – Zadania opisane w podstawie programowej na CKE

Doprowadź wyrażenie do najprostszej postaci: \(-\frac{1}{2}:0,25+5,25:0,05-7\frac{1}{2}\cdot \left( 2,5-3\frac{2}{3} \right)+1,25=\)

Zapisz obwód i pole trójkąta o bokach: a, a+2, b .

Rozwiąż równanie wyznaczając niewiadomą x. \[\frac{x-2}{3}=4\] \[\frac{x-2}{3}\quad -\quad \frac{3x-2}{2}=\quad 1\]

Długość kratki wynosi 1. Oblicz pola podanych figur.

Wyznacz liczbę całkowitą „a” dla której spełniona jest nierówność: \(a\le \sqrt{137}<a+1\)

Bartek i Grześ zbierali kasztany. Bartek zebrał n kasztanów, Grześ zebrał 7 razy więcej. Następnie Grześ w drodze do domu zgubił 10 kasztanów, a połowę pozostałych oddał Bartkowi. Ile kasztanów ma teraz Bartek, a ile ma Grześ?

Sprawdź, które liczby całkowite niedodatnie i większe od -8 są rozwiązaniem równania \(\frac{{{x}^{3}}}{8}+\frac{{{x}^{2}}}{2}=0\)

I. Samochód Tomasza na 100km spala 5 litrów benzyny, zatem mając w baku 8,6litra benzyny może on pokonać 150km. PRAWDA/FAŁSZ
II. 10dag wędliny kosztuje 23zł. Zatem 32zł wystarczy, aby kupić 1kg tej wędliny.PRAWDA/FAŁSZ
III. Romek przeczytał 250stron książki w ciągu 4dni. Jeśli będzie czytał w tym samym tempie to dokończenie książki czyli 300 stron zajmie mniej niż 6dni.PRAWDA/FAŁSZ

Dany jest ostrokątny trójkąt równoramienny ABC, w którym AC=BC. W tym trójkącie poprowadzono wysokość AD. Udowodnij, że kąt ACB jest dwa razy większy od kąta BAD.

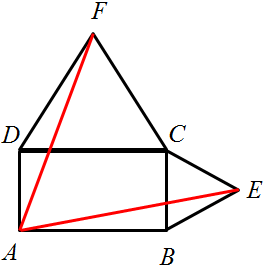
Na bokach BC i CD prostokąta ABCD zbudowano, na zewnątrz dwa trójkąty równoboczne BCE i CDF. Udowodnij, że AE=AF.

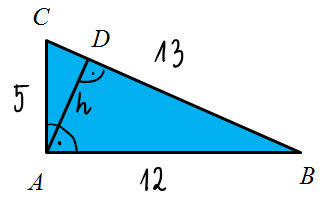
Oblicz najkrótszą wysokość trójkąta prostokątnego o bokach długości: 5cm, 12cm i 13cm.

Przekątne rombu ABCD mają długości AC = 8 dm i BD = 10 dm. Przekątną BD rombu przedłużono do punktu E w taki sposób, że odcinek BE jest dwa razy dłuższy od tej przekątnej. Oblicz pole trójkąta CDE. (zadanie ma dwie odpowiedzi).

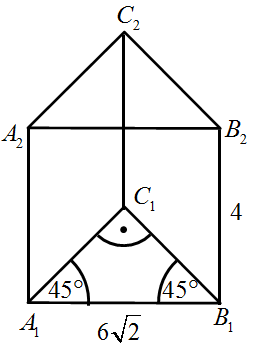
Podstawą graniastosłupa prostego jest trójkąt równoramienny, którego dwa równe kąty mają po 45°, a najdłuższy bok ma długość \(6\sqrt{2}dm\). Jeden z boków prostokąta, który jest w tym graniastosłupie ścianą boczną o największej powierzchni, ma długość 4 dm. Oblicz objętość i pole powierzchni całkowitej tego graniastosłupa.

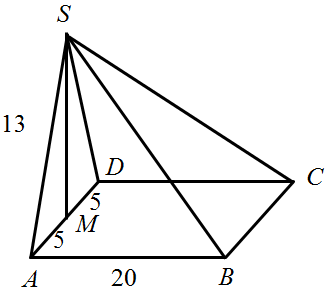
Prostokąt ABCD jest podstawą ostrosłupa ABCDS, punkt M jest środkiem krawędzi AD, odcinek MS jest wysokością ostrosłupa. Długość krawędzi: AD=10cm, AS=13cm oraz AB=20cm. Oblicz objętość ostrosłupa.

W klasie jest 14 dziewczynek i 11 chłopców. Na ile sposobów można wybrać z tej klasy dwuosobową delegację składającą się z jednej dziewczynki i jednego chłopca?

Z urny zawierającej kule ponumerowane liczbami od 1 do 7 losujemy bez zwracania dwie kule. Oblicz prawdopodobieństwo tego, że suma liczb na wylosowanych kulach będzie parzysta.