Figury geometryczne
Zadania, które ćwiczą własności i wzory związane z figurami geometrycznymi przed egzaminem ósmoklasisty.
Geometria – zadania na egzamin ósmoklasisty
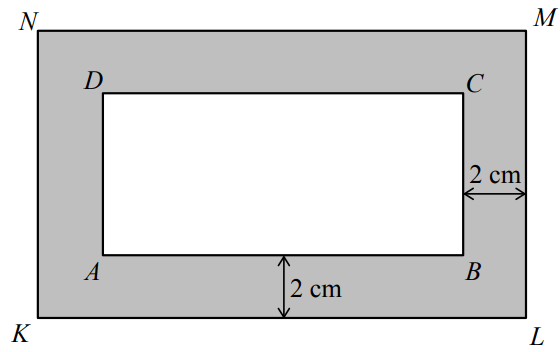
Prostokątna ramka ma szerokość 2 cm oraz |KL| =15 cm, |NK| = 9 cm (patrz rysunek).
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Prostokąty ABCD i KLMN są podobne. PRAWDA/FAŁSZ
Obwód prostokąta ABCD jest o 8 cm mniejszy od obwodu prostokąta KLMN. PRAWDA/FAŁSZ
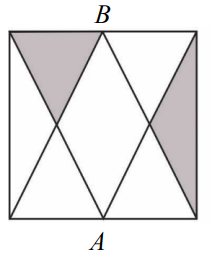
Punkty A i B są środkami boków kwadratu o polu 36a2.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Suma pól zacieniowanych części kwadratu jest równa:
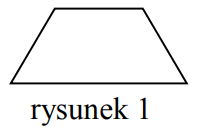
W ośrodku szkoleniowym są jednakowe stoliki, których blaty mają kształt trapezów równoramiennych, jak przedstawiono na rysunku 1.
Stoliki można ze sobą łączyć na różne sposoby. Na rysunkach przedstawiono trzy przykładowe zestawienia stolików w stoły konferencyjne oraz sposoby ustawienia przy nich krzeseł.
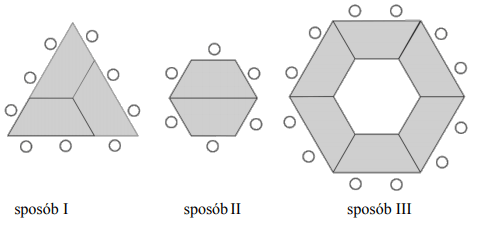
W ośrodku jest 36 stolików. Postanowiono je ustawić w jeden z trzech sposobów pokazanych na powyższych rysunkach.
Które z poniższych zdań jest fałszywe? Wybierz właściwą odpowiedź spośród podanych.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Kąty trapezu przedstawionego na rysunku 1 mają miary: 60°, 60°, 120°, 120°. PRAWDA/FAŁSZ
Krótsza podstawa tego trapezu jest 2 razy mniejsza od jego dłuższej podstawy. PRAWDA/FAŁSZ
Dwa boki pewnego trójkąta mają długości 12 cm i 15 cm.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Na kwadratowej siatce narysowano pewien wielokąt (patrz rysunek). Jego wierzchołki znajdują się w punktach przecięcia linii siatki.
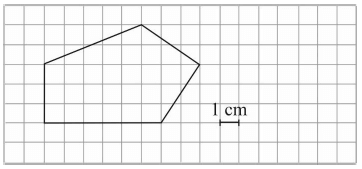
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole tego wielokąta jest równe
Na rysunku przedstawiono dwie figury. Figura I powstała przez usunięcie dwóch kwadratów jednostkowych z kwadratu o boku długości 6, a figura II powstała przez usunięcie dwóch kwadratów jednostkowych z prostokąta o bokach długości 4 i 8.
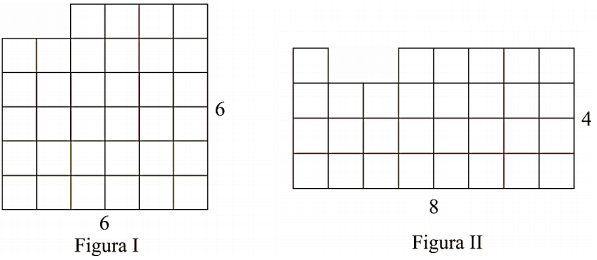
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Prostokąt o wymiarach \(3\sqrt{3}\)cm i \(5\sqrt{3}\)cm podzielono na 15 jednakowych kwadratów.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole jednego kwadratu jest równe:
Z kwadratu odcięto trójkąty tak, że linie cięcia przeprowadzono przez środki boków tego kwadratu (rysunek I). Z odciętych trójkątów ułożono trójkąt ABC (rysunek II).
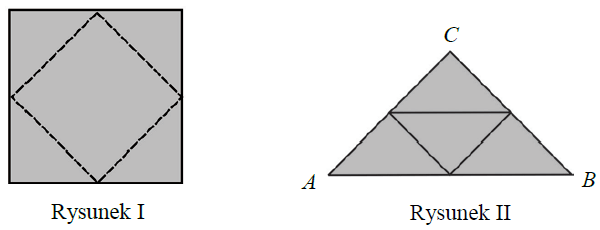
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Dwie przecinające się proste utworzyły cztery kąty. Suma miar trzech z tych kątów jest równa 225°.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Każdy bok kwadratu ABCD podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano ośmiokąt (rysunek).
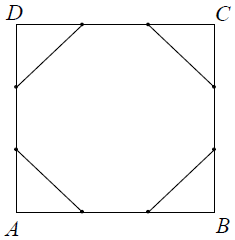
Które z poniższych zdań jest prawdziwe? Wybierz właściwą odpowiedź spośród podanych.
Ewa narysowała kwadrat o boku 1, prostokąt o bokach 2 i 1 oraz kąt prosty o wierzchołku O.
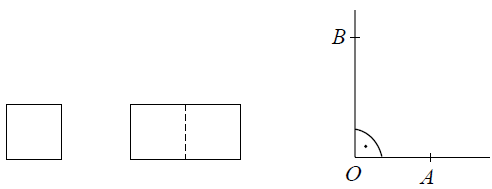
Następnie od wierzchołka O kąta prostego odmierzyła na jednym ramieniu kąta odcinek OA o długości równej przekątnej kwadratu, a na drugim ramieniu – odcinek OB o długości równej przekątnej prostokąta.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość odcinka AB jest równa
Wskazówka: Jest to bardzo ciekawe zadanie wykorzystujące twierdzenie Pitagorasa
Punkty E i F są środkami boków BC i CD kwadratu ABCD (rysunek).
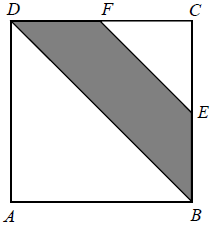
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli zdanie jest fałszywe.
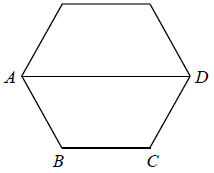
W układzie współrzędnych narysowano sześciokąt foremny o boku 2 tak, że jednym z jego wierzchołków jest punkt (0, 0), a jeden z jego boków leży na osi x (rysunek).
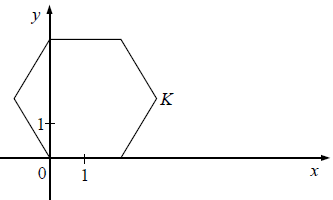
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Współrzędne wierzchołka K tego sześciokąta są równe
Do sześciokąta przedstawionego na rysunku w zadaniu 12. dorysowujemy kolejne takie same sześciokąty. Umieszczamy je tak, jak na rysunku, aby każdy następny sześciokąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego sześciokąta leżał na osi x. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, sześciokąty, które ponumerowano kolejnymi liczbami naturalnymi.
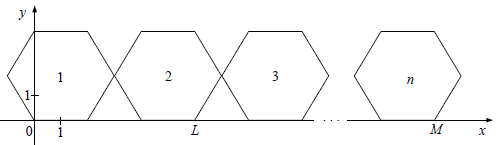
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli zdanie jest fałszywe.
Na rysunku przedstawiono sześciokąt foremny o boku równym 2 cm. Przekątna AD dzieli go na dwa przystające trapezy równoramienne.
Treść dostępna po opłaceniu abonamentu.
Ania wycięła z kartki papieru dwa jednakowe trójkąty prostokątne o bokach długości 12 cm, 16 cm i 20 cm. Pierwszy z nich zagięła wzdłuż symetralnej krótszej przyprostokątnej, a drugi – wzdłuż symetralnej dłuższej przyprostokątnej. W ten sposób otrzymała czworokąty pokazane na rysunkach.
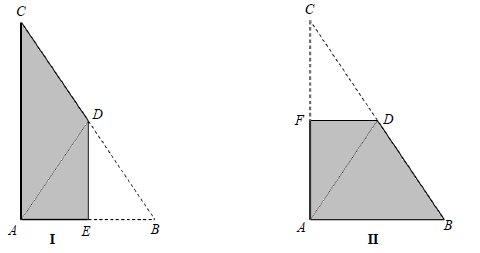Treść dostępna po opłaceniu abonamentu.
Jeżeli a, b i c są długościami boków trójkąta oraz c jest najdłuższym bokiem, to ten trójkąt jest:
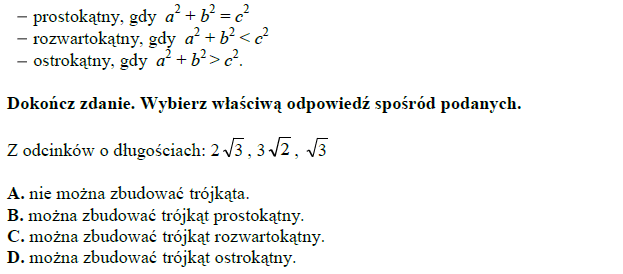Treść dostępna po opłaceniu abonamentu.
W równoległoboku ABCD bok AB jest dwa razy dłuższy od boku AD. Punkt K jest środkiem boku AB, a punkt L jest środkiem boku CD.
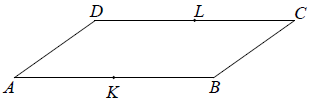
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Treść dostępna po opłaceniu abonamentu.
Pole zamalowanego trójkąta jest równe
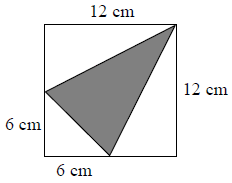
A. 108 cm2 B. 72 cm2 C. 54 cm2 D. 36 cm2
Treść dostępna po opłaceniu abonamentu.Wieża Eiffla znajduje się na obszarze w kształcie kwadratu o boku długości 125 m. Ile hektarów powierzchni ma ten obszar? Zapisz obliczenia. Wynik podaj z dokładnością do 0,1 ha.
Treść dostępna po opłaceniu abonamentu.Przed przystąpieniem do budowy latawca Janek rysuje jego model. Model ten przedstawiono na rysunku w skali 1:10. Oblicz pole powierzchni latawca zbudowanego przez Janka, wiedząc, że długości odcinków AC i BD równe są odpowiednio 4cm i 2cm, oraz AC⊥BD i S – środek BD. Zapisz obliczenia.
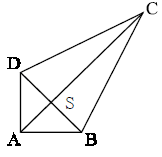Treść dostępna po opłaceniu abonamentu.