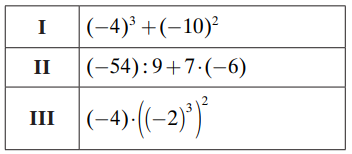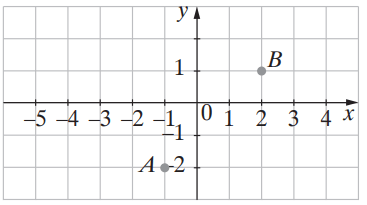Egzamin próbny ósmoklasisty z matematyki z Operonem 2019/2020

Odpowiedz na pytanie. Wybierz właściwą odpowiedź spośród podanych.
Jakim ułamkiem liczby 3,5 jest liczba 5?

Dane jest wyrażenie (2x − 3) (x + 3) − (x − 1)².

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Po doprowadzeniu do najprostszej postaci danego wyrażenia otrzymamy:

Dane jest równanie \(\frac{x}{2}+1=\frac{x}{3}\).
Jaka liczba jest rozwiązaniem tego równania? Wybierz właściwą odpowiedź spośród podanych.

Czy liczby 216 i 621 są wielokrotnościami tej samej nieparzystej liczby dwucyfrowej?
Wybierz odpowiedź T lub N i jej uzasadnienie spośród A, B albo C.

W tabeli podano trzy wyrażenia.

Które wyrażenia z tabeli mają wartość ujemną? Wybierz właściwą odpowiedź spośród podanych.

W pewnej szkole co szósty uczeń klasy ósmej deklaruje, że będzie kontynuował edukację w technikum. W tej szkole jest 21 takich uczniów.
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.

Do danej szkoły uczęszcza A/B uczniów klas ósmych.

Uczniowie, którzy chcą się uczyć w technikum, stanowią C/D niż 20% wszystkich ósmoklasistów tej szkoły.

Blokada rowerowa ma zapięcie z szyfrowanym zamkiem z trzema zapadkami. Na każdej z zapadek można ustawić cyfry od 0 do 9. Szyfr otwierający zamek tej blokady tworzą trzy cyfry, które są kolejnymi liczbami parzystymi.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli fałszywe.

Prawdopodobieństwo, że pierwszą cyfrą szyfru jest cyfra 0, wynosi \(\frac{1}{9}\). PRAWDA / FAŁSZ

Istnieją trzy możliwości wyboru szyfru dla zamka w takiej blokadzie. PRAWDA / FAŁSZ

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość wyrażenia \(3a-{{a}^{2}}\) dla \(a=\sqrt{5}\) w przybliżeniu do całości jest równa:

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Jeśli Kamil jedzie rowerem ze średnią prędkością 18 km/h, a Agata na hulajnodze elektrycznej pokonuje każde 400 m w ciągu minuty, to znaczy, że:

Dany jest kwadrat o polu powierzchni 48 cm².
Odpowiedz na pytanie. Wybierz właściwą odpowiedź spośród podanych.
Ile wynosi długość przekątnej tego kwadratu?

Dany jest trapez KLMN, w którym boki LM i MN są przystające, a przekątna LN jest prostopadła do boku KN.

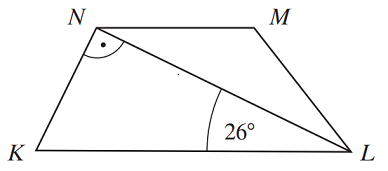
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.

Kąt ostry NKL ma miarę 64°. PRAWDA / FAŁSZ

Trapez KLMN jest trapezem równoramiennym. PRAWDA / FAŁSZ

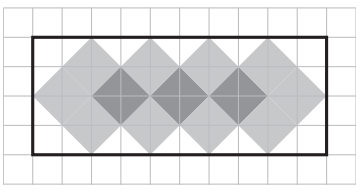
Prostokąt przedstawiony na rysunku został częściowo pomalowany.

Jaki procent prostokąta został pomalowany? Wybierz właściwą odpowiedź spośród podanych.

Kolejne liczby wstawiono do poniższej tabeli w pewien uporządkowany sposób. W przedstawionej tabeli brakuje jednej liczby.

Jakiej liczby brakuje w tabeli? Wybierz właściwą odpowiedź spośród podanych.

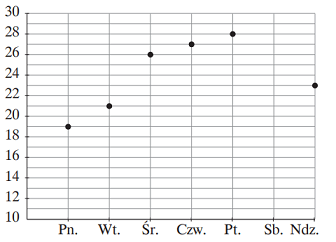
Wykres przedstawia temperatury w stopniach Celsjusza, jakie odnotowano w wybranym tygodniu lipca. Temperatura w sobotę wynosiła tyle, ile średnia temperatura z pozostałych dni tygodnia.

Jaką temperaturę odnotowano w danym tygodniu w sobotę? Wybierz właściwą odpowiedź spośród podanych.

Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.

Na mapie, która pomniejsza 600 tys. razy, rzeczywista odległość 150 km będzie odcinkiem o długości A/B.

Na planie wykonanym w skali C/D budynek o rzeczywistej długości 28 m to odcinek o długości 3,5 cm.

W prostokątnym układzie współrzędnych dane są dwa punkty: A= (-1,-2) i B =(2,1).

Czy punkt B leży w kole o środku w punkcie A i promieniu r = 4? Odpowiedź uzasadnij.

W prostokącie o obwodzie 98 cm stosunek długości sąsiednich boków wynosi 2 : 5.

Oblicz pole tego prostokąta. Zapisz obliczenia.

W kole narysowano cięciwę o długości 10 cm, a jej końce połączono odcinkami ze środkiem koła, tak że powstał trójkąt, którego jeden z kątów ma miarę 120°.

Oblicz, jaką długość ma promień tego koła. Zapisz obliczenia.

Łączny koszt zakupu dwóch książek o różnych tytułach wynosił 82 zł. Do biblioteki zakupiono po 5 sztuk każdej z nich w promocyjnej cenie o 20% niższej. Koszt zakupu pierwszego tytułu wyniósł 152 zł.

Oblicz cenę każdej z książek przed promocją. Zapisz obliczenia.

Firma remontowa otrzymała zlecenie na położenie nowych podłóg w dwóch mieszkaniach o łącznej powierzchni 159 m². W pierwszym mieszkaniu wyłożono już 24 m² nowej podłogi, co stanowi \(\frac{3}{8}\) powierzchni podłogi w tym mieszkaniu. W drugim natomiast pozostała jeszcze do położenia tylko podłoga w pokoju o wymiarach 3,8 x 5m.

Czy firma położyła już podłogę na \(\frac{2}{3}\) powierzchni w obu mieszkaniach? Odpowiedź uzasadnij. Zapisz obliczenia.

W ostrosłupie prostym podstawą jest romb o przekątnych 10 cm i 24 cm. Wysokość ostrosłupa jest dwa razy dłuższa niż bok rombu.

Oblicz objętość tego ostrosłupa. Zapisz obliczenia.