Egzamin próbny ósmoklasisty z matematyki z Operonem 2018/2019
Bartek wyruszył rowerem na trasę o długości 70 km o godzinie 8.20. Trasę tę pokonał, jadąc ze średnią prędkością 28 km/h. W trakcie jazdy, o godzinie 9.50, Bartek zrobił sobie piętnastominutową przerwę.
Uzupełnij zdania. Wybierz właściwą odpowiedź spośród A lub B oraz spośród C lub D.
Bartek zrobił sobie przerwę po przejechaniu A/B.
Bartek dojechał do końca trasy o godzinie C/D.
Na rysunku przedstawiono kartkę z kalendarza na rok 2019.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
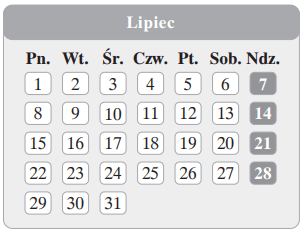
Druga niedziela czerwca 2019 r. przypadnie w dziewiątym dniu miesiąca. PRAWDA/FAŁSZ
Pierwszy dzień września w 2019 r. wypadnie w niedzielę. PRAWDA/FAŁSZ
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
W prostokątnym układzie współrzędnych punkt \(K=\left( -\sqrt{3}+2\sqrt{2},3\sqrt{2}-2\sqrt{3} \right)\) leży w:
Dane jest równanie: v−4(3 − 2x)= − 2,05+5x+(− 0,5)2
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Rozwiązaniem danego równania jest liczba:
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
60% liczby 4,5 wynosi tyle samo, co \(\frac{2}{3}\) liczby 4,05. PRAWDA/FAŁSZ
Liczba 2,7 jest o 10% większa od liczby 2\(\frac{3}{5}\). PRAWDA/FAŁSZ
Według przepisu do wykonania koktajlu owocowego dla 3 osób należy przygotować 30 dag truskawek.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Ilość truskawek, jaką zgodnie z przepisem trzeba przygotować do wykonania koktajlu dla 10 osób, można obliczyć za pomocą wyrażenia:
Gosia kupiła dwie cebulki kwiatów. Obie zasadzi w jednej doniczce. Ma do dyspozycji trzy doniczki ceramiczne i dwie plastikowe.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Gosia może zasadzić kwiaty w doniczkach na 6 różnych sposobów. PRAWDA/FAŁSZ
Prawdopodobieństwo, że obie cebulki Gosia zasadzi w doniczce ceramicznej, wynosi \(\frac{1}{5}\). PRAWDA/FAŁSZ
Na osi liczbowej zaznaczono zbiór liczb spełniających pewien warunek.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zaznaczony zbiór to wszystkie liczby:
Czy romb jest równoległobokiem? Wybierz odpowiedź T (tak) lub N (nie) i jej uzasadnienie spośród A, B albo C.

Uzupełnij zdania. Wybierz właściwą odpowiedź spośród A lub B oraz spośród C lub D.
Wyrażenie \({{\sqrt[3]{a}}^{2}}\) przyjmuje wartość 9 dla A/B.Wartość iloczynu \(\sqrt{8}\cdot 2\sqrt{2}\) wynosi C/D.
Dla zachowania bezpieczeństwa kąt nachylenia między poziomym podłożem a drabiną przystawną powinien wynosić od 65° do 75°.
Odpowiedz na pytanie. Wybierz właściwą odpowiedź spośród podanych.
Na którym rysunku przedstawiono ustawienie drabiny zgodne z wymaganiami bezpieczeństwa?
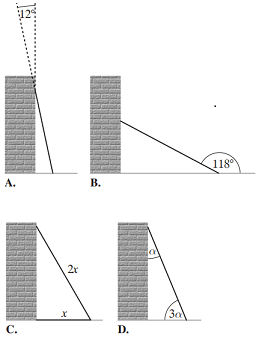
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Objętość prostopadłościanu o wymiarach 3 cm x 0,3 dm x 0,03 m wynosi:
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
W pewnym trójkącie dwa kąty mają miary po 35°. Oznacza to, że trójkąt ten jest:
Dane są liczby x = 2a + b – 3 oraz y = – 4(a – b) + 1.
Uzupełnij zdania. Wybierz właściwą odpowiedź spośród A lub B oraz spośród C lub D.
Suma liczb x i y wynosi A/B.
Różnica liczb y i x wynosi C/D.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Każdy graniastosłup prosty, który ma sześć ścian, jest prostopadłościanem. PRAWDA/FAŁSZ
Ostrosłup, który ma sześć krawędzi, jest czworościanem.
PRAWDA/FAŁSZ
Oblicz sumę wszystkich czynników pierwszych liczby 9350, jeżeli największy z nich wynosi 17.
Uzasadnij, że prostokąt o przekątnej długości 8 cm i szerokości \(4\sqrt{2}\)cm jest kwadratem.
Wojtek przechowuje 24 standardowe sześcienne kostki do gry w zamkniętym pudełku o pojemności 0,6 litra. Każda z tych kostek ma krawędź o długości 1,5 cm.
Oblicz, ile procent pojemności pudełka wypełniają wszystkie te kostki. Zapisz obliczenia.
Siostry Basia i Kasia zbierają pieniądze na wycieczkę. Basia uzbierała 115% kwoty, którą zebrała Kasia. Gdy każda dziewczynka dostała od dziadków dodatkowo po 232 zł, okazało się, że kwota uzbierana przez Kasię stanowi 92% kwoty zebranej przez Basię.
Oblicz, ile pieniędzy uzbierała każda z dziewcząt. Zapisz obliczenia.
Na rysunku I przedstawiono graniastosłup prawidłowy, którego wszystkie krawędzie są przystające, a suma ich długości wynosi 90 cm. Na II rysunku przedstawiono graniastosłup, który ma w podstawie trójkąt prostokątny o przyprostokątnych długości 6 cm i 8 cm. Obie bryły mają taką samą wysokość.
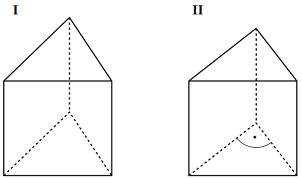
Oba te graniastosłupy połączono w taki sposób, że otrzymano jeden graniastosłup czworokątny.
Oblicz pole powierzchni całkowitej otrzymanego graniastosłupa czworokątnego. Zapisz obliczenia.




