Egzamin ósmoklasisty z matematyki 2020 CKE – dodatkowy – czerwiec
W tabeli przedstawiono fragment cennika, który obowiązuje w wypożyczalni gier planszowych „Świat Gier”.
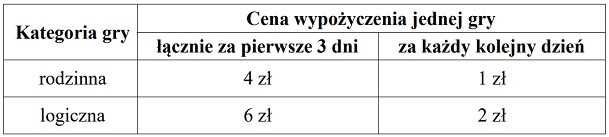
W tej wypożyczalni Janek wypożyczył jedną grę rodzinną i dwie gry logiczne na siedem dni.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Janek za wypożyczenie tych gier zapłacił
Dane są trzy wyrażenia arytmetyczne:
Które spośród tych wyrażeń mają wartość większą od 100? Wybierz właściwą odpowiedź spośród podanych.
W sklepie obniżono o 15% ceny wszystkich książek. Zosia wybrała książkę, która przed obniżką kosztowała 45 zł.
Ile zapłaci Zosia za tę książkę? Wybierz właściwą odpowiedź spośród podanych.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Na osi liczbowej między liczbami \(\left( -\frac{2}{6} \right)\quad oraz\quad \left( -\frac{1}{6} \right)\) znajduje się liczba
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Piechur i kolarz wyruszyli naprzeciw siebie na spotkanie tą samą drogą. Droga, która ich dzieliła, miała długość 48 km. Piechur wyszedł o \({{8}^{00}}\) i szedł ze stałą prędkością \(4\frac{km}{h}.\) Kolarz wyjechał o \({{10}^{00}}\) i jechał ze stałą prędkością \(16\frac{km}{h}.\)
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
O godzinie \({{10}^{30}}\) piechura i kolarza dzieliła droga o długości 30 km. P/F
Piechur i kolarz spotkają się o godzinie \({{12}^{00}}\). P/F
W pewnej klasie przeprowadzono ankietę na temat liczby rodzeństwa uczniów tej klasy. Okazało się, że 44% liczby uczniów ma siostrę, 72% – brata, a 4 uczniów ma i siostrę, i brata. Każdy uczeń tej klasy ma rodzeństwo.
Ilu uczniów brało udział w ankiecie? Wybierz właściwą odpowiedź spośród podanych.
Zależność drogi od czasu i przyśpieszenia w ruchu jednostajnie przyśpieszonym (gdy prędkość początkowa jest równa 0) opisuje wzór \(s=\frac{a{{t}^{2}}}{2},\) gdzie s – droga, t – czas, a – przyśpieszenie.
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wartość wyrażenia \({{\left( -2 \right)}^{4}}:{{\left( -2 \right)}^{3}}\) jest równa A/B
Wartość wyrażenia \({{\left( -2 \right)}^{2}}\cdot {{\left( -2 \right)}^{3}}\) jest równa C/D
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wartość wyrażenia \(\sqrt{36+64}\) jest równa A/B
Wartość wyrażenia \(\sqrt{1+\frac{9}{16}}\) jest równa C/D
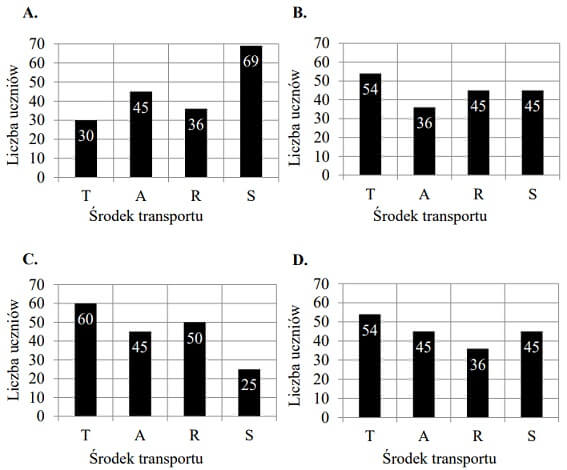
Wśród 180 uczniów dojeżdżających do szkoły przeprowadzono ankietę. Uczniowie odpowiadali na pytanie, z jakiego środka transportu korzystają w drodze do szkoły. Każdy uczeń wskazał jeden środek transportu. Otrzymano następujące wyniki: 30% uczniów dojeżdża tramwajem (T),\(\frac{1}{4}\) uczniów – autobusem (A), co piąty – rowerem (R), a pozostali – samochodem (S).
Na którym diagramie przedstawiono wyniki tej ankiety? Wybierz właściwą odpowiedź spośród podanych.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Na drewnianej kostce w kształcie sześcianu zaznaczono punkty K i L tak, jak na rysunku
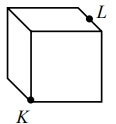
Po ścianach tej kostki od punktu K do punktu L przeszła mrówka.
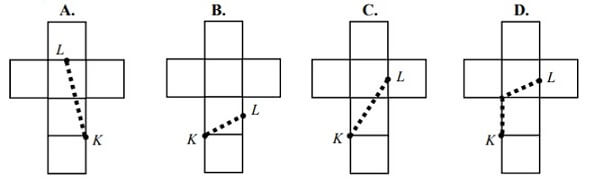
Na której z poniższych siatek sześcianu przedstawiono trasę, której nie mogła pokonać mrówka? Wybierz właściwą odpowiedź spośród podanych.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Uczniowie klasy 8a utworzyli jeden szereg, a uczniowie klasy 8b – drugi. W obu szeregach chłopcy i dziewczęta stali na przemian: chłopiec – dziewczyna – chłopiec – dziewczyna itd. W klasie 8a na pierwszym i ostatnim miejscu stali chłopcy, a w klasie 8b na pierwszym i ostatnim miejscu stały dziewczęta. W klasie 8a jest 12 dziewcząt, a w klasie 8b jest o dwóch chłopców mniej niż w klasie 8a.
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
W klasie 8a jest A/B chłopców.
W klasie 8b jest C/D uczniów.
Krótsza przekątna trapezu prostokątnego dzieli go na dwa trójkąty prostokątne równoramienne.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Wysokość trapezu i krótsza podstawa trapezu mają taką samą długość. P/F
Wysokość trapezu jest równa połowie dłuższej podstawy trapezu. P/F
W trójkącie prostokątnym o kącie ostrym 30° suma długości krótszej przyprostokątnej i przeciwprostokątnej jest równa 12 cm.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dłuższa przyprostokątna tego trójkąta ma długość
Na rysunku przedstawiono czworokąt ABCD, który podzielono na dwa trójkąty. Długości boków otrzymanych trójkątów opisano za pomocą wyrażeń algebraicznych. Obwód trójkąta ABC jest równy 31.
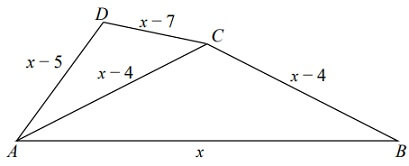
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Odcinek AC jest o 4 jednostki dłuższy od odcinka CD P/F
Obwód trójkąta ACD jest równy 23. P/F
Trzy proste przecinają się w punktach A, B i C tak, jak pokazano na rysunku. Odcinki AC i BC są równej długości. Wykaż, że miara kąta α stanowi połowę miary kąta β.
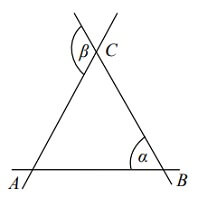 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Czworokąt ABCD jest trapezem. Podstawa AB została przedłużona do punktu E. Długości niektórych odcinków w tym czworokącie opisano na rysunku.
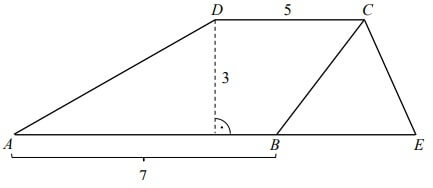
Pole trapezu ABCD jest trzy razy większe od pola trójkąta BEC. Oblicz długość odcinka BE. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Rada rodziców na nagrody dla dwóch klas ósmych przeznaczyła 1080 zł. W klasie 8a jest 32 uczniów, a w klasie 8b jest 28 uczniów. Pieniądze podzielono proporcjonalnie do liczby uczniów w danej klasie. Oblicz kwotę, jaką każda z klas otrzymała na nagrody. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Do pracowni komputerowej kupiono 6 myszek bezprzewodowych i 6 myszek przewodowych. Cena myszki bezprzewodowej była o 11 zł wyższa od ceny myszki z przewodem. Za zakup wszystkich myszek zapłacono 234 zł. Ile najwięcej myszek bezprzewodowych można by kupić za tę kwotę? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Dwa jednakowe prostopadłościany, każdy o wymiarach 5 cm, 7 cm i 9 cm, sklejono tak, jak pokazano na rysunku.
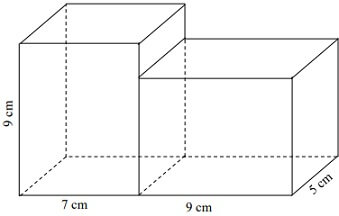
Oblicz pole powierzchni całkowitej powstałej bryły. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Pani Maria w 2015 roku łącznie zarobiła 43 740 zł. W każdym miesiącu od stycznia do września włącznie otrzymywała pensję tej samej wysokości. W październiku otrzymała podwyżkę, po której miesięcznie zarabiała 3780 zł. Oblicz, o ile procent wzrosła miesięczna pensja pani Marii po podwyżce. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.



