Egzamin gimnazjalny z matematyki 2018
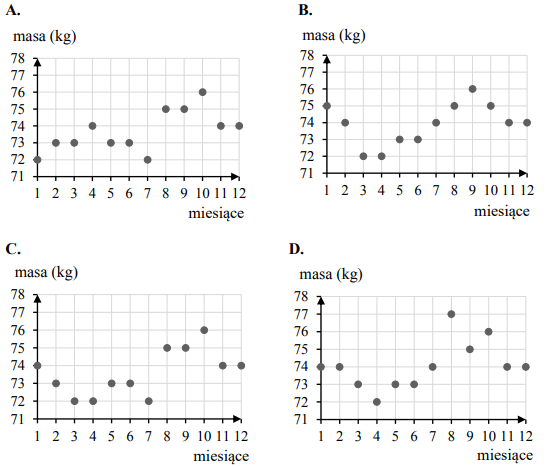
W pierwszym dniu każdego miesiąca ubiegłego roku pan Tomek zapisywał masę swojego ciała. Początkowo masa jego ciała malała. W listopadzie i grudniu ważył tyle samo, ile w lipcu. W żadnym miesiącu nie ważył więcej niż 76 kg. Pan Tomek wyniki swoich pomiarów umieścił na diagramie.
Który z diagramów przedstawia wyniki pomiarów pana Tomka w ubiegłym roku? Wybierz właściwą odpowiedź spośród podanych.
W ramach prac renowacyjnych odtworzono na ścianie budowli zegar słoneczny, który powstał w 1533 roku. Pod nowym zegarem zapisano datę tej renowacji – MCMXC.
Po ilu latach od powstania tego zegara słonecznego odtworzono go na ścianie budowli? Wybierz właściwą odpowiedź spośród podanych.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Samochód na pokonanie pierwszego odcinka trasy zużył 27 litrów benzyny. Na drugim odcinku trasy, mającym długość 150 km, zużył on dwa razy mniej benzyny niż na pierwszym odcinku. Średnie zużycie benzyny na kilometr było na każdym odcinku trasy takie samo.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Średnie zużycie benzyny przez ten samochód na każde 100 km tej trasy było równe
W czytelni ustawiono 20 stolików dwuosobowych i 10 stolików czteroosobowych. Po pewnym czasie 10% stolików dwuosobowych zastąpiono tą samą liczbą stolików czteroosobowych.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba stolików czteroosobowych zwiększyła się o
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Dane są dwie liczby:\(a={{8}^{5}},\,b={{4}^{5}}\)
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Iloraz \(\frac{\sqrt{12}}{\sqrt{75}\cdot \sqrt{3}}\) jest równy
Grupa turystów w ciągu pierwszej godziny marszu pokonała pewien odcinek trasy. W każdej następnej godzinie pokonywany dystans był o 0,5 km krótszy od dystansu pokonanego w poprzedniej godzinie. W ciągu pierwszych pięciu godzin marszu turyści przeszli łącznie
17,5 km trasy.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Odcinek trasy, który turyści przeszli w pierwszej godzinie marszu, miał długość
W autobusie jechało m mężczyzn i k kobiet. Na przystanku wysiedli 2 mężczyźni i 3 kobiety, a wsiadło 5 mężczyzn i 2 kobiety.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Gdy autobus odjechał z tego przystanku, podróżowało nim
Suma liczb x i y jest liczbą dodatnią, a ich iloczyn jest liczbą ujemną.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli
jest fałszywe.
Na rysunku przedstawiono dwie figury. Figura I powstała przez usunięcie dwóch kwadratów jednostkowych z kwadratu o boku długości 6, a figura II powstała przez usunięcie dwóch kwadratów jednostkowych z prostokąta o bokach długości 4 i 8.
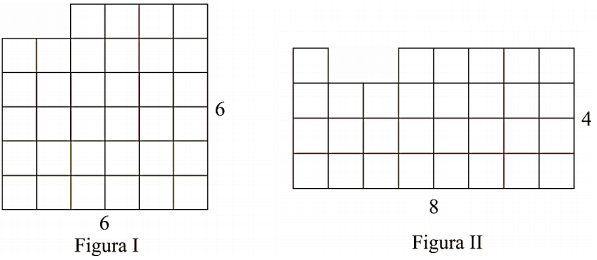
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
W pudełku są 2 kule zielone, 2 białe i 4 czarne. Losujemy z pudełka 1 kulę.
Czy prawdziwe jest stwierdzenie, że prawdopodobieństwo wylosowania kuli czarnej jest
równe \(\frac{1}{2}\)? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
W układzie współrzędnych zaznaczono dwa wierzchołki kwadratu MNPS, które nie należą do tego samego boku.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dwa pozostałe wierzchołki tego kwadratu mają współrzędne
W układzie współrzędnych narysowano wykres funkcji i zaznaczono jego punkty przecięcia z osiami układu.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Na kwadratowej siatce narysowano pewien wielokąt (patrz rysunek). Jego wierzchołki znajdują się w punktach przecięcia linii siatki.
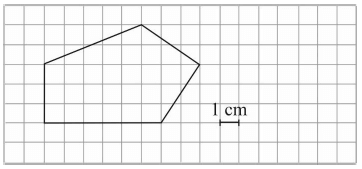
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole tego wielokąta jest równe
Dany jest trójkąt prostokątny ABC o przyprostokątnych długości 15 cm i 20 cm.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Przeciwprostokątna trójkąta DEF podobnego do trójkąta ABC w skali 2:1 ma długość
Dwa boki pewnego trójkąta mają długości 12 cm i 15 cm.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Na rysunku przedstawiono okrąg o środku O oraz kąt środkowy o mierze 280°. Punkty A i B znajdują się na okręgu. Prosta k jest styczna do okręgu w punkcie B.
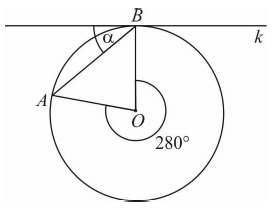
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miara kąta α jest równa
Na przekątnej BD kwadratu ABCD o boku długości 4 zbudowano trójkąt równoboczny BED.
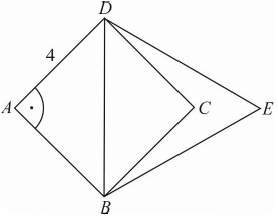
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole trójkąta BED jest równe
Pole podstawy walca jest równe 36π, a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wysokość tego walca jest równa
Do zestawu liczb: 3, 5 i 9 dopisano czwartą liczbę. Mediana otrzymanego w ten sposób zestawu czterech liczb jest większa od mediany początkowego zestawu trzech liczb. Uzasadnij, że dopisana liczba jest większa od 5.
Treść dostępna po opłaceniu abonamentu.Właściciel sklepu sportowego kupił w hurtowni deskorolki i kaski. Cena hurtowa deskorolki była o 60 zł wyższa niż cena hurtowa kasku. Właściciel sklepu ustalił cenę sprzedaży deskorolki o 20% wyższą od ceny hurtowej, a cenę sprzedaży kasku – o 40% wyższą od ceny hurtowej. Deskorolka i kask łącznie kosztowały w sklepie 397 zł. Oblicz łączny koszt zakupu po cenach hurtowych jednej deskorolki i jednego kasku. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Maja zrobiła dwa pudełka w kształcie graniastosłupów prawidłowych czworokątnych o różnych objętościach. Powierzchnię boczną każdego z tych graniastosłupów wykonała z takich samych prostokątów o wymiarach 28 cm i 12 cm (patrz rysunek). Oblicz różnicę objętości tych graniastosłupów. Zapisz obliczenia.
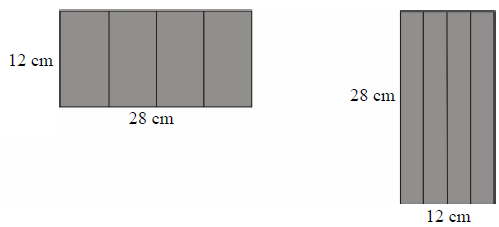 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.




