Dowody matematyczne przed egzaminem ósmoklasisty z matematyki
Dowody matematyczne pochodzące jeszcze z czasów gimnazjum, ale jak najbardziej odpowiadają poziomowi egzaminu ósmoklasisty. To bardzo dobry, a jednocześnie trudny materiał.
Dowody matematyczne
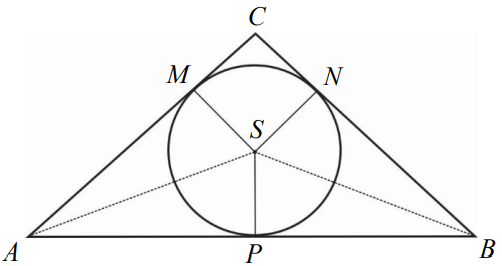
W trójkąt równoramienny ABC (|AC|= |BC|) wpisano okrąg o środku S. Punkty wspólne okręgu i trójkąta oznaczono literami M, N i P. Uzasadnij, że trójkąty ASM i PBS są przystające.
Zapisano trzy różne liczby, których średnia arytmetyczna jest równa 4, oraz dwie inne liczby, których średnia arytmetyczna jest równa 2. Uzasadnij, że średnia arytmetyczna zestawu tych pięciu liczb jest równa 3,2. Zapisz obliczenia.
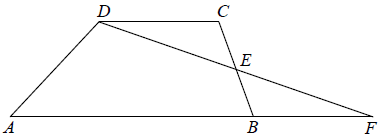
Na rysunku przedstawiono trapez ABCD i trójkąt AFD. Punkt E leży w połowie odcinka BC. Uzasadnij, że pole trapezu ABCD i pole trójkąta AFD są równe.
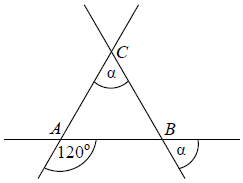
Trzy proste przecinające się w sposób przedstawiony na rysunku tworzą trójkąt ABC. Uzasadnij, że trójkąt ABC jest równoboczny.