Arkusz próbny ósmoklasisty z matematyki CKE 2018
Arkusz próbny ósmoklasisty z matematyki CKE 2018 – zadania i rozwiązania.
Firma przesyłkowa Wielpak korzysta z paczkomatów do samodzielnego nadawania i odbierania przesyłek przez klientów. Maksymalne wymiary prostopadłościennej paczki, którą można nadać za pośrednictwem tej firmy, wynoszą 38 cm × 41 cm × 64 cm, a masa przesyłki nie może być większa niż 25 kg.
W tabeli zapisano wymiary i masę czterech paczek.

Które z tych paczek mogą być nadane przez paczkomat tej firmy? Wybierz właściwą odpowiedź spośród podanych.
Poniżej zamieszczono fragment etykiety z jogurtu o masie 150 g.

Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz
odpowiedź spośród oznaczonych literami C i D.
Zjedzenie całego jogurtu dostarcza organizmowi około A/B wapnia
Zjedzenie całego jogurtu dostarcza organizmowi razy więcej białka niż C/D witaminy B2.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
120% liczby 180 to tyle samo, co 180% liczby 120. PRAWDA/FAŁSZ
20% liczby 36 to tyle samo, co 40% liczby 18. PRAWDA/FAŁSZ
Liczba x jest najmniejszą liczbą dodatnią podzielną przez 3 i 4, a liczba y jest największą liczbą dwucyfrową podzielną przez 2 i 9.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Najmniejsza wspólna wielokrotność liczb x i y jest równa
Na rysunku przedstawiono fragment podłogi pokrytej kaflami w kształcie kwadratów o boku długości 60 cm i kaflami w kształcie jednakowych prostokątów (patrz rysunek I). Na podłodze tej położono prostokątny dywan (patrz rysunek II).
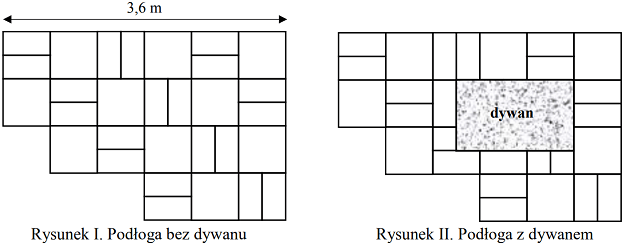
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Dywan ma powierzchnię większą niż powierzchnia 4 kwadratowych kafli.PRAWDA/FAŁSZ
Dywan ma wymiary 90 cm × 120 cm.PRAWDA/FAŁSZ
Prędkość rozchodzenia się impulsu elektrycznego u człowieka wynosi około 2 metrów na sekundę. U roślin impuls elektryczny może rozchodzić się z prędkością około 60 centymetrów na minutę.
Ile razy prędkość rozchodzenia się impulsu elektrycznego u człowieka jest większa od prędkości rozchodzenia się impulsu elektrycznego u roślin? Wybierz właściwą odpowiedź spośród podanych.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Monika poprawnie zaokrągliła liczbę 3465 do pełnych setek i otrzymała liczbę x, a Paweł poprawnie zaokrąglił liczbę 3495 do pełnych tysięcy i otrzymał liczbę y.
Czy liczby x i y są równe? Wybierz odpowiedź A (Tak) albo B (Nie) i jej uzasadnienie spośród 1, 2 albo 3.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Dana jest liczba \(a=3\sqrt{2}-4\).
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Liczba o 2 większa od liczby a jest równa A/B
Liczba 2 razy większa od liczby a jest równa C/D
Państwo Nowakowie mają trzy córki i jednego syna. Średnia wieku wszystkich dzieci państwa Nowaków jest równa 10 lat, a średnia wieku wszystkich córek jest równa 8 lat.
Ile lat ma syn państwa Nowaków? Wybierz właściwą odpowiedź spośród podanych
Do gry planszowej używane są dwa bączki o kształtach przedstawionych na rysunkach. Każdy bączek po zatrzymaniu na jednym boku wielokąta wskazuje liczbę umieszczoną na jego tarczy. Na rysunku I bączek ma kształt pięciokąta foremnego z zaznaczonymi liczbami od 1 do 5. Na rysunku II bączek ma kształt sześciokąta foremnego z zaznaczonymi liczbami od 1 do 6.
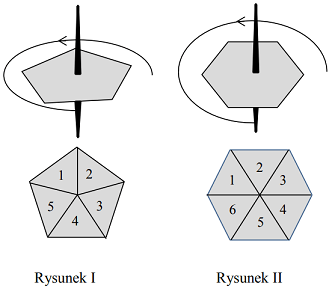
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Prawdopodobieństwo otrzymania liczby większej niż 3 na bączku z rysunku I jest większe niż \(\frac{1}{2}\)
PRAWDA/FAŁSZ
Uzyskanie nieparzystej liczby na bączku z rysunku I jest tak samo
prawdopodobne, jak uzyskanie nieparzystej liczby na bączku z rysunku II.PRAWDA/FAŁSZ
O liczbie x wiemy, że \(\frac{1}{3}\) tej liczby jest o \(\frac{3}{4}\) większa od \(\frac{1}{6}\) tej liczby.
Które równanie pozwoli wyznaczyć liczbę x ? Wybierz właściwą odpowiedź spośród podanych.
W trójkącie ABC największą miarę ma kąt przy wierzchołku C. Miara kąta przy wierzchołku A jest równa \(48{}^\circ \), a miara kąta przy wierzchołku B jest równa różnicy miary kąta przy wierzchołku C oraz miary kąta przy wierzchołku A.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Kąt przy wierzchołku B ma miarę \(48{}^\circ \).PRAWDA/FAŁSZ
Trójkąt ABC jest prostokątny.PRAWDA/FAŁSZ
W układzie współrzędnych zaznaczono dwa punkty: A = (−8, −4) i P = (−2, 2). Punkt P jest środkiem odcinka AB.
Jakie współrzędne ma punkt B? Wybierz właściwą odpowiedź spośród podanych.
Cztery jednakowe drewniane elementy, każdy w kształcie prostopadłościanu o wymiarach 2 cm × 2 cm × 9 cm, przyklejono do metalowej płytki w sposób pokazany na rysunku I.
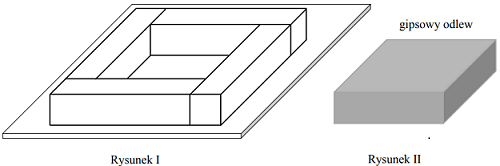
W ten sposób przygotowano formę, którą wypełniono masą gipsową, i tak otrzymano gipsowy
odlew w kształcie prostopadłościanu, pokazany na rysunku II.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz
odpowiedź spośród oznaczonych literami C i D.
Objętość drewna, z którego zbudowano formę, jest równa A/B
Objętość gipsowego odlewu jest równaC/D
Prostokąt ABCD o wymiarach 7 cm i 8 cm rozcięto wzdłuż prostej a na dwa trapezy tak, jak pokazano na rysunku. Odcinek CL ma długość 3,2 cm.
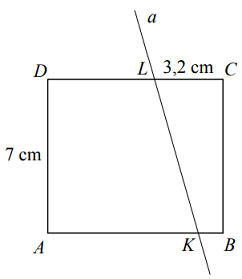
Pole trapezu KBCL jest czterokrotnie mniejsze od pola prostokąta ABCD. Oblicz długość odcinka KB. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Na pozalekcyjne zajęcia sportowe zapisanych jest 37 osób. Uzasadnij, że w tej grupie są co najmniej 4 osoby, które urodziły się w tym samym miesiącu.
Treść dostępna po opłaceniu abonamentu.Cztery jednakowe prostopadłościenne klocki, każdy o wymiarach 2 cm × 1 cm × 1 cm, ułożono tak, jak przedstawiono na rysunku.
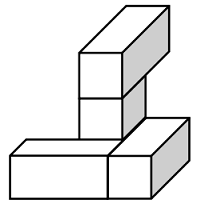
Następnie do tej budowli dołożono sześcienne klocki o krawędzi długości 1 cm tak, aby powstał prostopadłościan najmniejszy z możliwych.
Uzupełnij zdania. Wpisz w każdą lukę odpowiednią liczbę.
Liczba sześciennych klocków o krawędzi długości 1 cm, które należy dołożyć do budowli, jest równa ______. Najmniejszy z możliwych prostopadłościanów, który w ten sposób otrzymano, ma wymiary ___ cm × ___ cm × ___ cm.
Treść dostępna po opłaceniu abonamentu.Agata postanowiła przygotować kartkę okolicznościową w kształcie prostokąta, ozdobioną wzorem dokładnie takim, jak przedstawiony na rysunku. Kartka ta będzie miała wymiary 15 cm × 18 cm. Do jej ozdobienia Agata chce użyć jednakowych kwadratów, których bok wyraża się całkowitą liczbą centymetrów. Niektóre z tych kwadratów będzie musiała przeciąć na dwie lub na cztery jednakowe części.
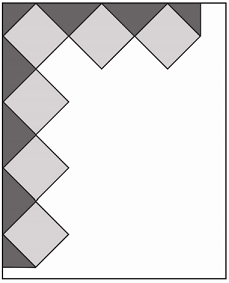
Oblicz maksymalną długość boku jednego kwadratu. Do obliczeń przyjmij przybliżenie \(\sqrt{2}\approx 1,4\). Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.W wyborach na przewodniczącego klasy kandydowało troje uczniów: Jacek, Helena i Grzegorz. Każdy uczeń tej klasy oddał jeden ważny głos. Jacek otrzymał 9 głosów, co stanowiło 36% wszystkich głosów. Helena otrzymała o 6 głosów więcej niż Grzegorz. Oblicz, ile głosów otrzymała Helena, a ile – Grzegorz. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Ania postanowiła pojechać autobusem do babci do miejscowości Sokółka. Z domu wyszła o godzinie 8:00, kilka minut czekała na przystanku, a następnie jechała autobusem. Do Sokółki dotarła o godzinie 9:30 i tam na przystanku spotkała się z babcią. Na wykresie w sposób uproszczony przedstawiono zależność prędkości, z jaką poruszała się Ania, od czasu.
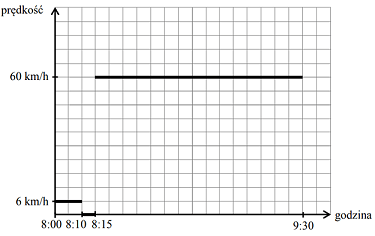
Oblicz długość trasy pokonanej przez Anię od wyjścia z domu do chwili spotkania z babcią. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.



