8 dniowa powtórka przed egzaminem ósmoklasisty CKE – 16.03.2020
Dzień 1 – Potęgi, pierwiastki, liczby
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Najmniejszą liczbą całkowitą większą od liczby \({{\left( -1\frac{2}{3} \right)}^{2}}\) jest
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Dane są liczby \(a=9\sqrt{2}\quad i\quad b=3\sqrt{2}.\)
Uzupełnij podane niżej zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Iloczyn liczb a i b jest równy A/B
Iloraz liczb a i b jest równy C/D
Oblicz wartość wyrażenia \(\frac{{{36}^{6}}}{{{27}^{5}}\cdot {{8}^{5}}}\)
Wskazówka: Zapisz wyrażenie w postaci potęg liczb 2 i 3.
Wykaż, że wartość wyrażenia \(\frac{21\sqrt{15}}{\sqrt{12}+5\sqrt{3}}\) jest liczbą mniejszą od 7.
Powierzchnię metali można chronić, stosując powłoki z innych metali, np. ze złota.
Blaszkę o powierzchni \(S=0,001\ {{m}^{2}}\)
pokryto warstwą złota o grubości y = 0,000001 m.
Gęstość złota wynosi: \(d=19\,300\ kg/{{m}^{3}}\)
Gęstość ciała wyraża się wzorem d = m/V, gdzie m jest masą ciała, a V jest jego objętością.
Oblicz masę złotej powłoki, którą pokryto blaszkę. Wynik zapisz w notacji wykładniczej: \(a\cdot {{10}^{k}}\quad gdzie\quad 1\le a<10\)
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Dzień 2 – Wyrażenia algebraiczne
Pan Jan spłacił całą pożyczkę w x ratach. Każda z pierwszych czterech rat była równa a zł, a każda z pozostałych była o 100 zł większa od pierwszej raty.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Spłaconą kwotę pożyczki opisano wyrażeniem
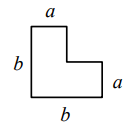
Na rysunku przedstawiono kształt i wymiary elementu układanki, w którym sąsiednie boki są do siebie prostopadłe.
Z takich elementów zbudowano dwie figury przedstawione na poniższym rysunku.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla x = 3 i y = –2 wartość 0 przyjmuje wyrażenie
Paweł zjada średnio a jabłek w czasie b dni.
Którym wyrażeniem opisano, ile średnio jabłek Paweł zjada w ciągu tygodnia? Wybierz właściwą odpowiedź spośród podanych.
Z każdego narożnika prostokąta odcięto kwadrat o boku a. Na rysunku przedstawiono wymiary otrzymanej figury (obszar zacieniowany).
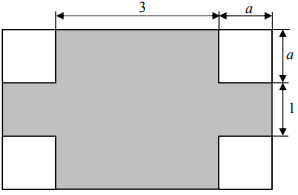
Zapisz wyrażenie algebraiczne opisujące pole zacieniowanej figury i oblicz jego wartość dla a = 2,5. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.
Nauczyciel zadał wszystkim uczniom w klasie następujące zadanie:
Pomyśl pewną liczbę, pomnóż ją przez 3, do iloczynu dodaj 6, a otrzymany wynik podziel
przez 3. Teraz od ostatniego wyniku odejmij liczbę, którą pomyślałeś na początku.
Uzasadnij, że każdy uczeń powinien otrzymać taki sam końcowy wynik.
Treść dostępna po opłaceniu abonamentu.Dzień 3 – Procenty
W kwietniu sprzedano 60 opakowań lodów, a w maju – 150 opakowań tych lodów.
O ile procent sprzedaż lodów była wyższa w maju niż w kwietniu? Wybierz właściwą odpowiedź spośród podanych.
Właściciel sklepu, sprzedając pewien towar po 75 zł za sztukę, zarabia 2% tej kwoty.
Ile sztuk tego towaru musi sprzedać, aby zarobić 300 zł? Wybierz właściwą odpowiedź spośród podanych.
W pewnej klasie przeprowadzono ankietę na temat liczby rodzeństwa uczniów tej klasy. Wszyscy uczniowie tej klasy wypełnili ankietę. Okazało się, że 44% liczby uczniów ma siostrę, 72% – brata, a 4 uczniów ma i siostrę, i brata. Każdy uczeń tej klasy ma rodzeństwo.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Długość boku kwadratu ABCD zwiększono o 12% i otrzymano kwadrat PRST.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Obwód kwadratu PRST jest większy od obwodu kwadratu ABCD o
Uczniowie klasy VII wybierali przewodniczącego swojej klasy. Było dwoje kandydatów: Ania i Bartek. Każdy z uczniów oddał jeden ważny głos. Ania uzyskała 56,25% wszystkich głosów, pokonując Bartka 4 głosami. Ilu uczniów wzięło udział w głosowaniu? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Sprzedawca rozważa dwie opcje obniżki ceny pewnego towaru. Która obniżka jest większa: od razu o 45%, czy: najpierw o 25%, a następnie o 20%? Odpowiedź uzasadnij. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Dzień 4 – Równania
W pojemniku znajdują się niebieskie, czarne i zielone piłeczki. Piłeczek czarnych jest o 20% mniej niż niebieskich, a niebieskich o 6 mniej niż zielonych. Niebieskich i zielonych piłeczek jest łącznie o 48 więcej niż czarnych. Przez n oznaczmy liczbę piłeczek niebieskich.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli
jest fałszywe.
Na rysunku przedstawiono trójkąt równoboczny i prostokąt oraz opisano za pomocą wyrażeń algebraicznych długości ich boków. Wielokąty mają równe obwody.
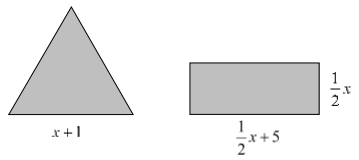
Uzupełnij podane niżej zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Długość boku trójkąta jest równa A/BEnergię kinetyczną Ek ciała o masie m poruszającego się z prędkością v można obliczyć ze wzoru: \({{E}_{k}}=\frac{m\cdot {{v}^{2}}}{2}\)
Którym równaniem opisano v poprawnie wyznaczone z tego wzoru? Wybierz właściwą odpowiedź spośród podanych.
Jeden z kątów w trójkącie ABC jest dwa razy większy od sumy miar dwóch pozostałych kątów tego trójkąta. Oblicz miarę największego kąta trójkąta ABC. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Dany jest trapez ABCD, którego dłuższa podstawa jest równa 10 cm, krótsza podstawa ma długość 6 cm, a jego wysokość jest równa 5 cm. Poprowadzono prostą EF równoległą do boku AD trapezu, w taki sposób, że pole trapezu EBCF jest trzy razy większe od pola równoległoboku AEFD. Oblicz długość odcinka AE.
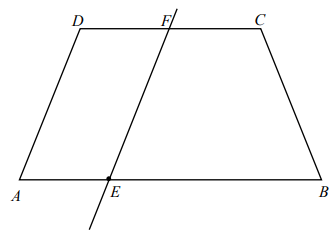Treść dostępna po opłaceniu abonamentu.
Adam i Basia w czasie wycieczki do Krakowa kupowali pamiątkowe magnesy w tym samym sklepie. Cena jednego magnesu z widokiem Wawelu była równa 2,50 zł, a cena jednego magnesu ze smokiem wawelskim 4,50 zł. Adam kupił magnesy z widokiem Wawelu i magnesy ze smokiem wawelskim, łącznie 12 sztuk. Zakupione przez Adama magnesy kosztowały 36 zł. Basia kupiła tylko magnesy ze smokiem wawelskim i zapłaciła za nie tyle, ile Adam za magnesy z widokiem Wawelu. Ile magnesów ze smokiem wawelskim kupiła Basia? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Na przedstawienie do teatru pojechały dzieci pod opieką dorosłych, przy czym dzieci było o 24 więcej niż dorosłych. Cena biletu dla osoby dorosłej wynosiła 40 zł, a cena biletu dla dziecka była o 45% niższa niż dla osoby dorosłej. Za wszystkie bilety zapłacono 900 zł. Ile łącznie biletów do teatru zakupiono? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Dzień 5 – Skala, wartości proporcjonalne, środek odcinka
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D. Na mapie wykonanej w skali 1 : 45 000 odległość między dwoma miastami wynosi 24 cm.
Rzeczywista odległość między tymi miastami wynosi A/B:Pan Bartek kupił 15 sadzonek kwiatów i zapłacił za nie 67,50 zł. Pan Michał kupił 50 sadzonek w tej samej cenie za jedną sztukę. O ile złotych więcej zapłacił za sadzonki pan Michał niż pan Bartek? Wybierz właściwą odpowiedź spośród podanych.
W tabeli podano informacje o dwóch rodzajach białej farby sprzedawanej w sklepie.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Paweł podzielił trasę wycieczki rowerowej na dwa etapy, między którymi przez kwadrans odpoczywał. Pierwszy etap miał długość 18 km i Paweł pokonał go w ciągu 36 minut. Drugi etap miał 6 km i Paweł pokonał go z taką samą prędkością średnią co pierwszy etap.
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Pokonanie drugiego etapu wycieczki zajęło Pawłowi A/B:
Czas, który upłynął od rozpoczęcia pierwszego etapu do zakończenia drugiego to C/D:
Dane są cztery liczby:
Które z tych liczb wybranych spośród I–IV znajdują się na osi liczbowej między liczbami \(\left( -5,5 \right)\ i\ \left( -5\frac{1}{3} \right)\)? Wybierz właściwą odpowiedź spośród podanych.
W układzie współrzędnych zaznaczono dwa punkty A=(−8,−4) i P=(−2,2). Punkt P jest środkiem odcinka AB. Jakie współrzędne ma punkt B? Wybierz właściwą odpowiedź spośród podanych.
Asia planuje upiec ciasteczka migdałowe. Zgodnie z przepisem do upieczenia porcji ciasteczek potrzebuje 250 g masła, 300 g mąki, 90 g cukru, 200 g migdałów i szczyptę soli. Asia ma tylko 120 g migdałów i chce je wszystkie wykorzystać do pieczenia, zachowując proporcje między składnikami podane w przepisie. Ile gramów masła, mąki i cukru powinna Asia przygotować? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Ola i Basia kupiły takie same cukierki na wagę. Basia za 36 dag cukierków zapłaciła 11,52 zł, a Ola za swoje zapłaciła 17,28 zł. Ile dekagramów cukierków kupiła Ola? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Ania sprawdziła, że odległość między Pragą a Rzymem na mapie wykonanej w skali 1:3000000 jest równa 30,8cm. Bartek natomiast sprawdził, że odległość między Wiedniem, a Paryżem na mapie wykonanej w skali 1:5000000 jest równa 20,7 cm. Uzasadnij, że Wiedeń i Paryż dzieli większa odległość niż Pragę i Rzym.
Treść dostępna po opłaceniu abonamentu.Dzień 6 – Wybrane własności figur
Na rysunku przedstawiono równoległobok ABCD.
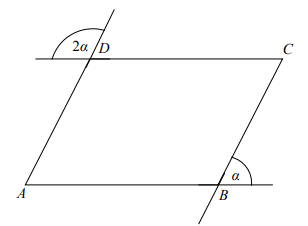
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Kąt BAD tego równoległoboku ma miarę
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wśród wszystkich takich trójkątów, których długości dwóch boków są równe 5 cm i 9 cm, istnieje trójkąt, którego trzeci bok ma długość:
Bok sześciokąta foremnego ma długość 12 cm.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli
jest fałszywe.
Na rysunku I przedstawiono blat stołu, który ma kształt sześciokąta i podano niektóre jego wymiary. Sześciokąt tworzą dwa przystające trapezy równoramienne złączone dłuższymi podstawami. Powierzchnię blatu stołu powiększono, dodając prostokątną wkładkę, w taki sposób, jak przedstawiono na rysunku II. Długość krótszego boku wkładki jest równa 0,54 m.
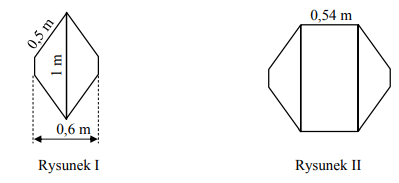
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Powierzchnia blatu stołu przedstawionego na rysunku I jest równa A/B :Bok kwadratu ma 12 cm. Każdy z boków kwadratu podzielono na 3 równe części. Sąsiednie punkty podziału połączono odcinkami i otrzymano ośmiokąt. Oblicz pole tego ośmiokąta. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Promień OA okręgu o środku w punkcie O ma długość 5 cm i tworzy z cięciwą AB kąt o mierze 45º. Oblicz długość cięciwy AB. Zapisz obliczenia.
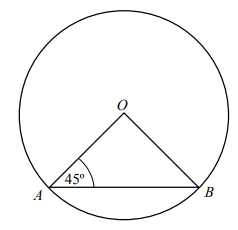Treść dostępna po opłaceniu abonamentu.
Dany jest trójkąt ABC. Punkt D jest środkiem boku BC. Uzasadnij, że odcinek łączący wierzchołek A z punktem D dzieli ten trójkąt na dwa trójkąty o jednakowych polach.
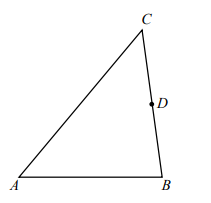Treść dostępna po opłaceniu abonamentu.
Pole rombu jest równe 96 cm2. Długość jednej z jego przekątnych stanowi 0,75 długości drugiej przekątnej. Oblicz obwód tego rombu. Zapisz obliczenia
Treść dostępna po opłaceniu abonamentu.Dzień 7 – Bryły
W ogrodzie na poziomej powierzchni stał pusty zbiornik w kształcie sześcianu o krawędzi długości 1 m. W czasie deszczu zgromadziła się w nim woda, która sięgała do wysokości 1,5 cm ponad dno zbiornika.
Ile litrów wody zgromadziło się w tym zbiorniku podczas deszczu? Wybierz właściwą odpowiedź spośród podanych.
Z jednakowych sześciennych kostek zbudowano prostopadłościan w taki sposób, jak przedstawiono na poniższym rysunku. Oznaczmy przez x pole powierzchni całkowitej każdej kostki.
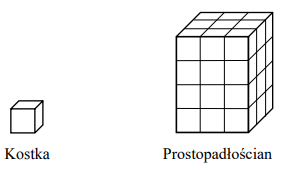Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.Pole powierzchni całkowitej zbudowanego prostopadłościanu jest równe
Ściana boczna graniastosłupa prawidłowego sześciokątnego jest kwadratem o polu 9cm2.
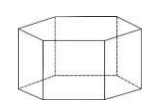Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli
jest fałszywe.
Dany jest ostrosłup pięciokątny i graniastosłup dziesięciokątny.
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Z wypełnionego wodą prostopadłościennego wazonu o wymiarach podstawy 12,5 cm i 16 cm odlano 0,5 litra wody. O ile cm obniżył się poziom wody w wazonie? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Zbiornik w kształcie graniastosłupa prawidłowego czworokątnego postawiono na ścianie, która nie jest kwadratem. Do zbiornika wlano 120 litrów wody, która sięgnęła do wysokości 5 dm. Jakie wymiary może mieć ten zbiornik, jeśli długość każdej jego krawędzi wyraża się całkowitą liczbą decymetrów większą od 2? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Podstawą ostrosłupa jest prostokąt o obwodzie 28 cm. Jeden z boków prostokąta jest dłuższy od drugiego o 2 cm. Wysokość ostrosłupa poprowadzona z wierzchołka S jest równa przekątnej podstawy. Oblicz objętość tego ostrosłupa. Zapisz obliczenia.
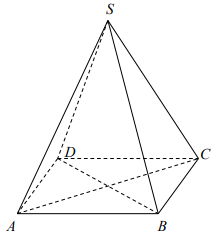Treść dostępna po opłaceniu abonamentu.
W fabryce mebli z kawałka drewna w kształcie prostopadłościanu o wymiarach 9cm, 12cm i 75cm wycinana jest noga do stołu (patrz rysunek). Noga taka ma kształt graniastosłupa o podstawie ośmiokąta. Podczas produkcji jednej nogi powstają odpady, którymi są cztery jednakowe kawałki drewna (oznaczone na rysunku szarym kolorem) o kształcie i wymiarach podanych na rysunku.
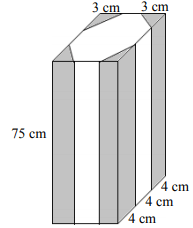Do produkcji nóg używane jest drewno, którego 1cm3 ma masę 0,5 g. W ciągu godziny produkuje się 15 takich nóg. Ile kilogramów odpadów wytwarzanych jest w tej fabryce w ciągu jednej godziny pracy? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.
Dzień 8 – Rachunek prawdopodobieństwa
Tosia buduje wieżę z trzech klocków: czerwonego, żółtego i niebieskiego, ustawiając je jeden na drugim w przypadkowej kolejności.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Prawdopodobieństwo tego, że klocek niebieski znajdzie się w środku, a na nim klocek czerwony, jest równe
Rzucamy standardową sześcienną kostką do gry.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba jeden jest wartością prawdopodobieństwa zdarzenia polegającego na tym, że w jednokrotnym rzucie kostką wypadnie
W pojemniku znajdują się kule zielone, czarne i białe. Liczba kul zielonych stanowi połowę liczby wszystkich kul.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
W pewnej firmie pracuje 5 osób. Średnia pensja w tej firmie jest równa 3200 złotych. Najmniej zarabia pan Jędrzej – jego pensja jest niższa niż 2700 złotych.
Czy prawdziwe jest stwierdzenie, że średnia pensja pozostałych czterech pracowników jest wyższa niż 3200 zł? Wybierz odpowiedź A. (Tak) albo B. (Nie) i jej uzasadnienie spośród zdań 1., 2. albo 3.
Treść dostępna po opłaceniu abonamentu.
Janek przez siedem kolejnych dni tygodnia o godzinie 18.00 mierzył temperaturę powietrza. Średnia arytmetyczna odczytanych przez niego temperatur z tych siedmiu dni wynosiła 2 ºC. Na poniższym diagramie zaznaczono sześć spośród siedmiu odczytanych przez Janka temperatur. Każda temperatura wyrażona jest liczbą całkowitą.
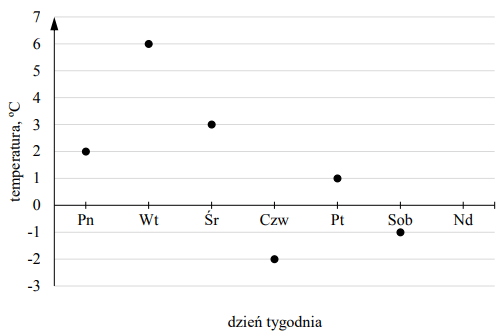
Jaką temperaturę Janek odczytał w niedzielę? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.W pudełku jest 18 kul ponumerowanych od 1 do 18, przy czym kule z numerami od 1 do 9 są pomalowane na czerwono, a pozostałe na zielono. Z tego pudełka wyciągamy losowo jedną kulę. Jakie jest prawdopodobieństwo, że będzie to kula zielona z numerem nieparzystym? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.W szkole Artura odbyły się trzy etapy rozgrywek w warcaby. Na każdym etapie za każdą grę można było uzyskać 0 punktów albo 1 punkt. W trzecim etapie rozgrywek drużyna Artura pięciokrotnie wygrała i zdobyła w sumie 5 punktów. Średnia liczba punktów zdobytych przez tę drużynę we wszystkich trzech etapach jest równa 4,0. Ile punktów mogła uzyskać drużyna Artura w pierwszym, a ile – w drugim etapie rozgrywek? Podaj wszystkie możliwości. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.W pudelku jest 10 kul, w tym 4 czarne i 6 białych. Franek z zamkniętymi oczami losuje z pudełka kolejno po jednej kuli i odkłada je na bok. Ile co najmniej kul musi wylosować, aby mieć pewność, że wśród wylosowanych kul będą dwie kule czarne? Odpowiedź uzasadnij
Treść dostępna po opłaceniu abonamentu.