Cecha podzielności przez 2, 3, 4, 5, 6, 7, 8, 9,10,11,12 itd
Cechy podzielności – co jest w artykule?
- Cechy podzielności
- Cecha podzielności przez 2
- Cecha podzielności przez 3
- Cecha podzielności przez 4
- Cecha podzielności przez 5
- Cecha podzielności przez 6
- Cecha podzielności przez 7
- Cecha podzielności przez 8
- Cecha podzielności przez 9
- Cecha podzielności przez 10
- Cecha podzielności przez 11
- Cecha podzielności przez 12
- Cecha podzielności przez 13
- Cecha podzielności przez 14
- Cecha podzielności przez 15
- Cecha podzielności przez 16
- Cecha podzielności przez 18
- Cecha podzielności przez 20
- Cecha podzielności przez 21
- Cecha podzielności przez 22
- Cecha podzielności przez 24
- Cecha podzielności przez 25
- Cecha podzielności przez 26
- Cecha podzielności przez 28
- Cecha podzielności przez 30
- Cecha podzielności przez 50
- Cecha podzielności przez 75
- Cecha podzielności przez 100
- Cecha podzielności przez 1000
- Cechy podzielności zadania standardowe
- Cechy podzielności zadania trudne
- Cechy podzielności zadania bardzo trudne
Cechy podzielności
Cecha podzielności przez 2
Cecha podzielności przez 2: Na końcu liczby znajduje się cyfra: 0, 2, 4, 6, 8.
Przykład: 124, 1200, 128, 299106 są podzielne przez 2, ponieważ na końcu znajduje się liczba parzysta.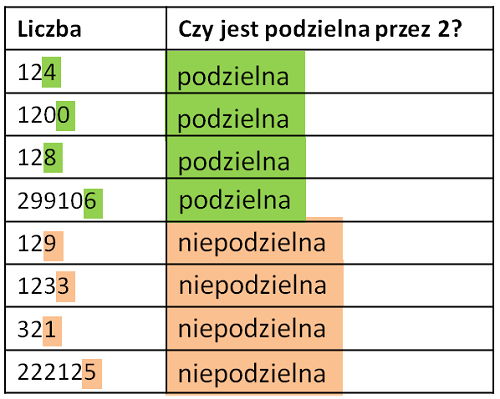
Przykład: 124, 1200, 128, 299106 są podzielne przez 2, ponieważ na końcu znajduje się liczba parzysta.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 3
Cecha podzielności przez 3: Suma cyfr danej liczby jest podzielna przez 3.
Przykład: 123 jest podzielne przez 3, ponieważ suma cyfr=1+2+3=6, a 6:3 dzieli się bez reszty. 111111111 jest podzielne przez 3, ponieważ suma cyfr=1+1+1+1+1+1+1+1+1=9, a 9:3 dzieli się bez reszty.
Przykład: 123 jest podzielne przez 3, ponieważ suma cyfr=1+2+3=6, a 6:3 dzieli się bez reszty. 111111111 jest podzielne przez 3, ponieważ suma cyfr=1+1+1+1+1+1+1+1+1=9, a 9:3 dzieli się bez reszty.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 4
Cecha podzielności przez 4: Ostatnie dwie cyfry danej liczby tworzą liczbę podzielną przez 4.
Przykład: 1372 jest podzielne przez 4, ponieważ ostatnie dwie cyfry tworzą liczbę 72, a liczba 72 dzieli się przez 4 bez reszty. 12224 jest podzielne przez 4, ponieważ ostatnie dwie cyfry tworzą liczbę 24, a liczba 24 dzieli się przez 4 bez reszty.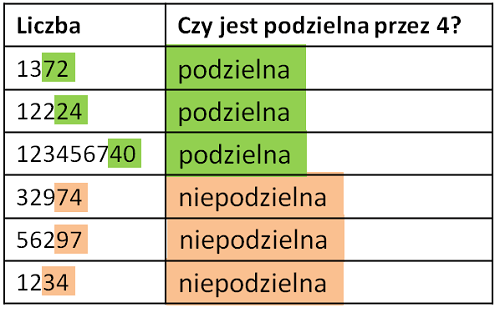
Przykład: 1372 jest podzielne przez 4, ponieważ ostatnie dwie cyfry tworzą liczbę 72, a liczba 72 dzieli się przez 4 bez reszty. 12224 jest podzielne przez 4, ponieważ ostatnie dwie cyfry tworzą liczbę 24, a liczba 24 dzieli się przez 4 bez reszty.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 5
Cecha podzielności przez 5: Ostatnią cyfrą w liczbie jest 0 lub 5.
Przykład: 1205 jest podzielne przez 5, ponieważ na końcu jest cyfra 5. 13260 jest podzielne przez 5, ponieważ na końcu jest cyfra 0.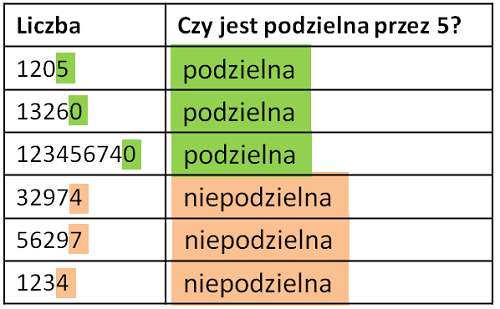
Przykład: 1205 jest podzielne przez 5, ponieważ na końcu jest cyfra 5. 13260 jest podzielne przez 5, ponieważ na końcu jest cyfra 0.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 6
Cecha podzielności przez 6: Liczba spełnia jednocześnie cechę podzielności przez 2 i przez 3.
Przykład: 123228 dzieli się przez 6, ponieważ jest spełniona cecha podzielności przez 2 (na końcu jest liczba parzysta 8) i cecha podzielności przez 3 (suma cyfr=1+2+3+2+2+8=18, zaś 18 dzieli się przez 3 bez reszty).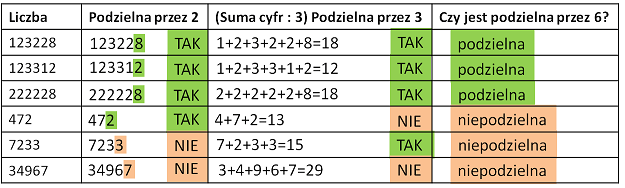
Przykład: 123228 dzieli się przez 6, ponieważ jest spełniona cecha podzielności przez 2 (na końcu jest liczba parzysta 8) i cecha podzielności przez 3 (suma cyfr=1+2+3+2+2+8=18, zaś 18 dzieli się przez 3 bez reszty).

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 7
Cecha podzielności przez 7: Suma cyfr danej liczby pomnożona (od prawej) przez kolejne potęgi 3 (włącznie z potęgą zerową: 30=1) jest podzielna przez 7.
Przykład: 609 dzieli się przez 7, ponieważ 6·32+0·31+9·30=54+0+9=63, zaś liczba 63 jest podzielna przez 7 bez reszty. 10206 dzieli się przez 7, ponieważ 1·34+0·33+2·32+0·31+6·30=81+0+18+0+6=105, zaś liczba 105 jest podzielna przez 7 bez reszty.
Przykład: 609 dzieli się przez 7, ponieważ 6·32+0·31+9·30=54+0+9=63, zaś liczba 63 jest podzielna przez 7 bez reszty. 10206 dzieli się przez 7, ponieważ 1·34+0·33+2·32+0·31+6·30=81+0+18+0+6=105, zaś liczba 105 jest podzielna przez 7 bez reszty.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 8
Cecha podzielności przez 8: Ostatnie trzy cyfry tworzą liczbę podzielną przez 8.
Przykład: 11048 jest podzielne przez 8 ponieważ ostatnie 3 cyfry tworzą liczbę 048, czyli 48, zaś 48:8 dzieli się bez reszty. 6120 jest podzielne przez 8 ponieważ ostatnie 3 cyfry tworzą liczbę 120, zaś 120:8 dzieli się bez reszty.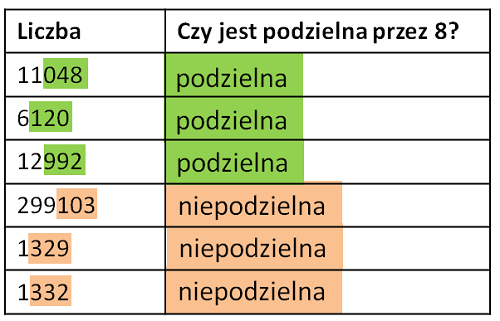
Przykład: 11048 jest podzielne przez 8 ponieważ ostatnie 3 cyfry tworzą liczbę 048, czyli 48, zaś 48:8 dzieli się bez reszty. 6120 jest podzielne przez 8 ponieważ ostatnie 3 cyfry tworzą liczbę 120, zaś 120:8 dzieli się bez reszty.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 9
Cecha podzielności przez 9: Suma cyfr danej liczby jest podzielna przez 9.
Przykład: 987654321 jest podzielne przez 9, ponieważ suma cyfr tej liczby=45 , zaś 45:9 bez reszty 1221354 jest podzielne przez 9, ponieważ suma cyfr tej liczby=18 , zaś 18:9 bez reszty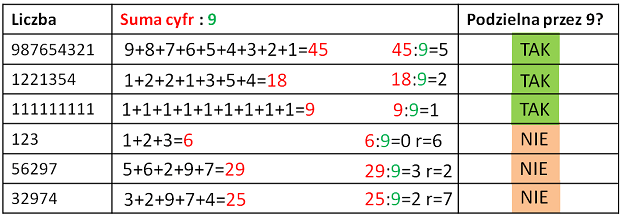
Przykład: 987654321 jest podzielne przez 9, ponieważ suma cyfr tej liczby=45 , zaś 45:9 bez reszty 1221354 jest podzielne przez 9, ponieważ suma cyfr tej liczby=18 , zaś 18:9 bez reszty

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 10
Cecha podzielności przez 10: Ostatnia cyfra liczby to 0.
Przykład: 11610 dzieli się przez 10, ponieważ na ostatnim miejscu jedności jest 0. 610 dzieli się przez 10, ponieważ na końcu liczby jest 0.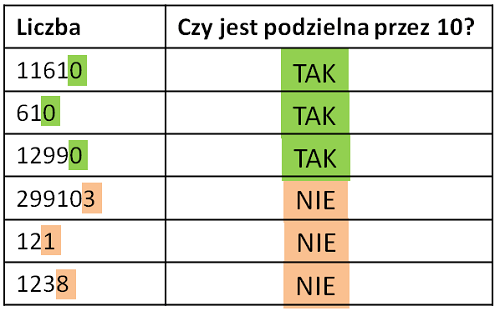
Przykład: 11610 dzieli się przez 10, ponieważ na ostatnim miejscu jedności jest 0. 610 dzieli się przez 10, ponieważ na końcu liczby jest 0.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 11
Cecha podzielności przez 11: Po odjęciu sumy cyfr na miejscach parzystych, sumy cyfr stojących na miejscach nieparzystych otrzymamy wynik podzielny przez 11.(Miejsca parzyste lub nieparzyste możemy liczyć dowolnie: od lewej lub prawej strony).
Przykład: 605070807 jest liczbą podzielną przez 11, ponieważ licząc sumę cyfr na miejscach nieparzystych od strony lewej otrzymujemy 6+5+7+8+7=33, zaś licząc sumę cyfr na miejscach parzystych od strony lewej otrzymujemy 0+0+0+0=0. Różnica otrzymanych sum 33-0=33 jest podzielna przez 11 bez reszty. Zauważ, że licząc sumy cyfr od strony prawej otrzymasz różnicę 0-33=-33, a ta liczba również dzieli się przez 11 bez reszty tylko, że wynik jest ujemny. 91272596833 jest liczbą podzielną przez 11, ponieważ licząc sumę cyfr na miejscach nieparzystych od strony lewej otrzymujemy 9+2+2+9+8+3=33, zaś licząc sumę cyfr na miejscach parzystych od strony lewej otrzymujemy 1+7+5+6+3=22. Różnica otrzymanych sum 33-22=11 jest podzielna przez 11 bez reszty.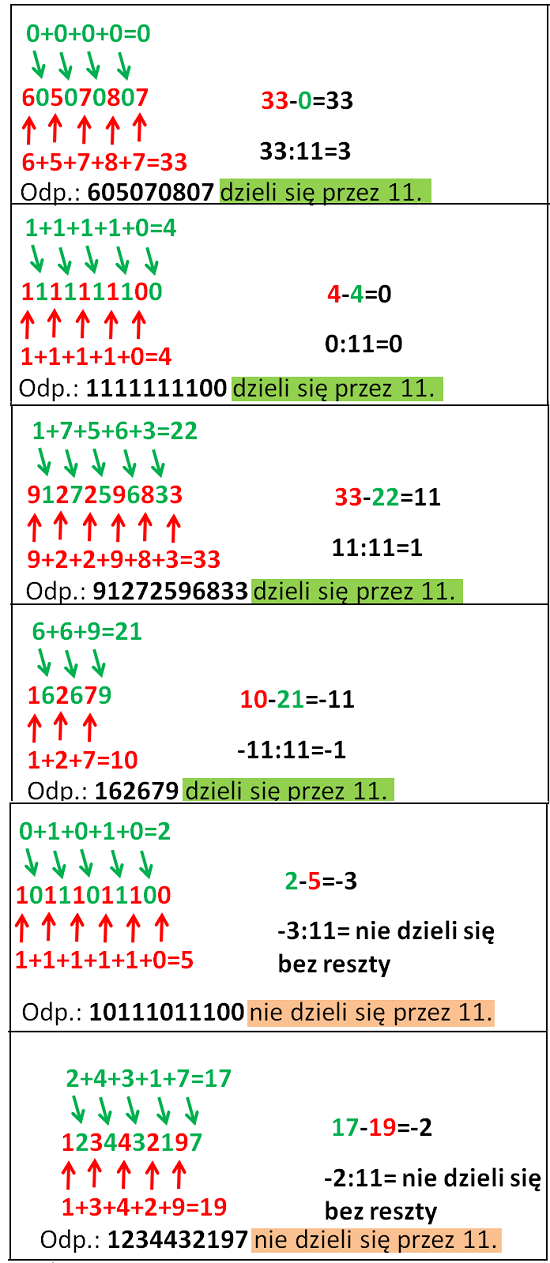
Przykład: 605070807 jest liczbą podzielną przez 11, ponieważ licząc sumę cyfr na miejscach nieparzystych od strony lewej otrzymujemy 6+5+7+8+7=33, zaś licząc sumę cyfr na miejscach parzystych od strony lewej otrzymujemy 0+0+0+0=0. Różnica otrzymanych sum 33-0=33 jest podzielna przez 11 bez reszty. Zauważ, że licząc sumy cyfr od strony prawej otrzymasz różnicę 0-33=-33, a ta liczba również dzieli się przez 11 bez reszty tylko, że wynik jest ujemny. 91272596833 jest liczbą podzielną przez 11, ponieważ licząc sumę cyfr na miejscach nieparzystych od strony lewej otrzymujemy 9+2+2+9+8+3=33, zaś licząc sumę cyfr na miejscach parzystych od strony lewej otrzymujemy 1+7+5+6+3=22. Różnica otrzymanych sum 33-22=11 jest podzielna przez 11 bez reszty.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 12
Cecha podzielności przez 12:
Liczba spełnia jednocześnie cechę podzielności przez 3 i przez 4.
Przykład: 124224 jest podzielne przez 4, ponieważ ostatnie dwie cyfry tworzą liczbę 24, która dzieli się przez 4 bez reszty. Dana liczba jest także podzielna przez 3, ponieważ suma cyfr=1+2+4+2+2+4=15 jest podzielna przez 3 bez reszty. Z podzielności przez 4 i 3 wynika podzielność przez 12. 123312 jest podzielne przez 4, ponieważ ostatnie dwie cyfry tworzą liczbę 12, która dzieli się przez 4 bez reszty. Dana liczba jest także podzielna przez 3, ponieważ suma cyfr=1+2+3+3+1+2=12 jest podzielna przez 3 bez reszty. Z podzielności przez 4 i 3 wynika podzielność przez 12.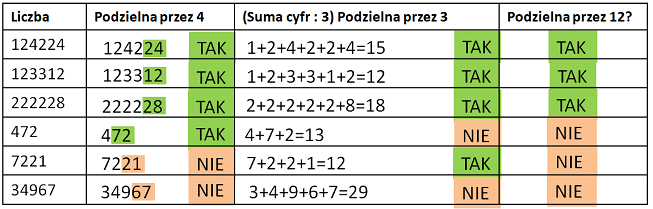
Liczba spełnia jednocześnie cechę podzielności przez 3 i przez 4.
Przykład: 124224 jest podzielne przez 4, ponieważ ostatnie dwie cyfry tworzą liczbę 24, która dzieli się przez 4 bez reszty. Dana liczba jest także podzielna przez 3, ponieważ suma cyfr=1+2+4+2+2+4=15 jest podzielna przez 3 bez reszty. Z podzielności przez 4 i 3 wynika podzielność przez 12. 123312 jest podzielne przez 4, ponieważ ostatnie dwie cyfry tworzą liczbę 12, która dzieli się przez 4 bez reszty. Dana liczba jest także podzielna przez 3, ponieważ suma cyfr=1+2+3+3+1+2=12 jest podzielna przez 3 bez reszty. Z podzielności przez 4 i 3 wynika podzielność przez 12.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 13
Cecha podzielności przez 13: Różnica liczby złożonej z trzech ostatnich cyfr i liczby złożonej z pozostałych cyfr jest podzielna przez 13.
Przykład: 7033 jest podzielna przez 13, ponieważ różnica liczby zbudowanej z trzech ostatnich cyfr:033 i liczby zbudowanej z pozostałych cyfr:7. Otrzymana różnica:33-7=26 jest podzielna przez 13 bez reszty. 207831 jest podzielna przez 13, ponieważ różnica liczby zbudowanej z trzech ostatnich cyfr:831 i liczby zbudowanej z pozostałych cyfr:207. Otrzymana różnica:831-207=624. Liczba 624 jest podzielna przez 13 bez reszty.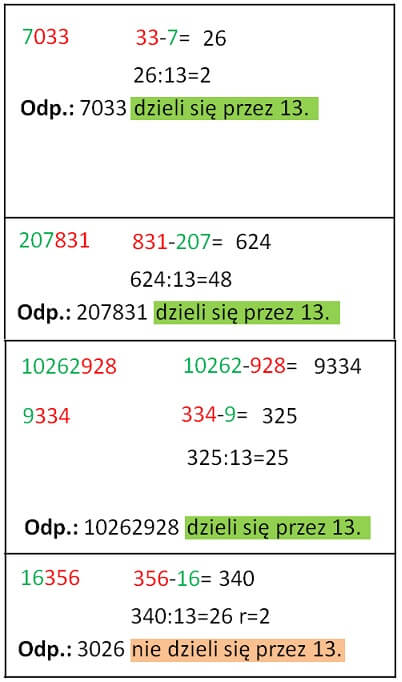
Przykład: 7033 jest podzielna przez 13, ponieważ różnica liczby zbudowanej z trzech ostatnich cyfr:033 i liczby zbudowanej z pozostałych cyfr:7. Otrzymana różnica:33-7=26 jest podzielna przez 13 bez reszty. 207831 jest podzielna przez 13, ponieważ różnica liczby zbudowanej z trzech ostatnich cyfr:831 i liczby zbudowanej z pozostałych cyfr:207. Otrzymana różnica:831-207=624. Liczba 624 jest podzielna przez 13 bez reszty.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 14
Cecha podzielności przez 14:
Liczba spełnia jednocześnie cechę podzielności przez 2 i przez 7.
Przykład: 1078 jest podzielna przez 2, bo na ostatnim miejscu jedności jest liczba parzysta. 1078 dzieli się przez 7, ponieważ 1·33+0·32+7·31+8·30=27+0+21+8=56, zaś liczba 56 jest podzielna przez 7 bez reszty. 10052 jest podzielna przez 2, bo na ostatnim miejscu jedności jest liczba parzysta. 10052 dzieli się przez 7, ponieważ 1·34+0·33+0·32+5·31+2·30=81+0+0+15+2=98, zaś liczba 98 jest podzielna przez 7 bez reszty.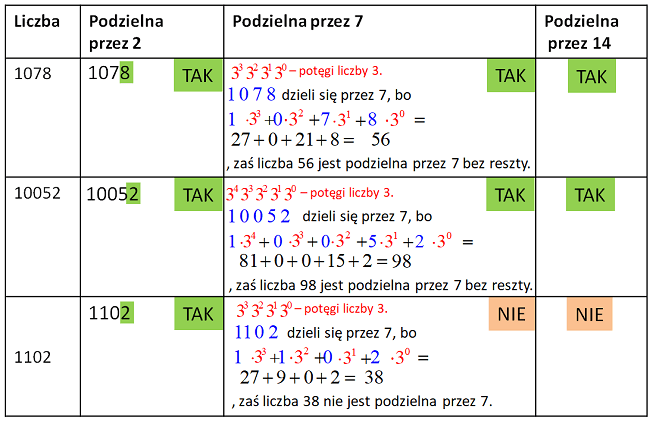
Liczba spełnia jednocześnie cechę podzielności przez 2 i przez 7.
Przykład: 1078 jest podzielna przez 2, bo na ostatnim miejscu jedności jest liczba parzysta. 1078 dzieli się przez 7, ponieważ 1·33+0·32+7·31+8·30=27+0+21+8=56, zaś liczba 56 jest podzielna przez 7 bez reszty. 10052 jest podzielna przez 2, bo na ostatnim miejscu jedności jest liczba parzysta. 10052 dzieli się przez 7, ponieważ 1·34+0·33+0·32+5·31+2·30=81+0+0+15+2=98, zaś liczba 98 jest podzielna przez 7 bez reszty.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 15
Cecha podzielności przez 15:
Liczba spełnia jednocześnie cechę podzielności przez 3 i przez 5.
Przykład: 225 jest podzielne przez 5, bo na ostatnim miejscu jest cyfra 5. Dana liczba jest też podzielna przez 3, ponieważ suma cyfr=2+2+5=9 dzieli się przez 3 bez reszty. 480 jest podzielne przez 5, bo na ostatnim miejscu jest cyfra 0. Dana liczba jest też podzielna przez 3, ponieważ suma cyfr=4+8+0=12 dzieli się przez 3 bez reszty.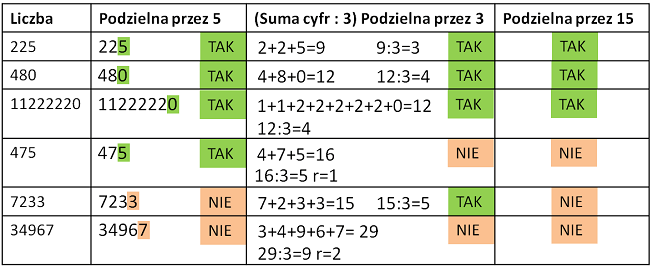
Liczba spełnia jednocześnie cechę podzielności przez 3 i przez 5.
Przykład: 225 jest podzielne przez 5, bo na ostatnim miejscu jest cyfra 5. Dana liczba jest też podzielna przez 3, ponieważ suma cyfr=2+2+5=9 dzieli się przez 3 bez reszty. 480 jest podzielne przez 5, bo na ostatnim miejscu jest cyfra 0. Dana liczba jest też podzielna przez 3, ponieważ suma cyfr=4+8+0=12 dzieli się przez 3 bez reszty.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 16
Cecha podzielności przez 16:
Cztery ostatnie cyfry tworzą liczbę, która jest podzielna przez 16.
Przykład: 20064 jest podzielne przez 16, ponieważ cztery ostatnie cyfry tworza liczbę 0064, która jest podzielna przez 16 bez reszty. 210048 jest podzielne przez 16, ponieważ cztery ostatnie cyfry tworza liczbę 0048, która jest podzielna przez 16 bez reszty.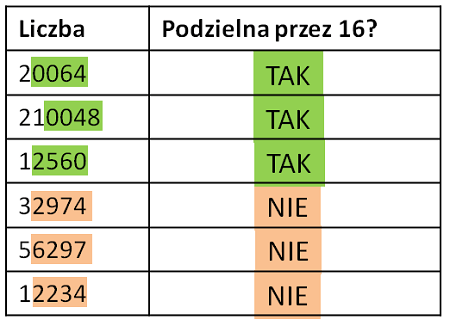
Cztery ostatnie cyfry tworzą liczbę, która jest podzielna przez 16.
Przykład: 20064 jest podzielne przez 16, ponieważ cztery ostatnie cyfry tworza liczbę 0064, która jest podzielna przez 16 bez reszty. 210048 jest podzielne przez 16, ponieważ cztery ostatnie cyfry tworza liczbę 0048, która jest podzielna przez 16 bez reszty.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 18
Cecha podzielności przez 18:
Liczba spełnia jednocześnie cechę podzielności przez 2 i przez 9.
Przykład: 1242 jest podzielna przez 2, ponieważ ostatnia cyfra jest parzysta oraz jest podzielna przez 9, bo suma cyfr=1+2+4+2=9 dzieli się przez 9 bez reszty. Z podzielności przez 2 i przez 9 wynika podzielność liczby przez 18. 993312 jest podzielna przez 2, ponieważ ostatnia cyfra jest parzysta oraz jest podzielna przez 9, bo suma cyfr=9+9+3+3+1+2=27 dzieli się przez 9 bez reszty. Z podzielności przez 2 i przez 9 wynika podzielność liczby przez 18.
Liczba spełnia jednocześnie cechę podzielności przez 2 i przez 9.
Przykład: 1242 jest podzielna przez 2, ponieważ ostatnia cyfra jest parzysta oraz jest podzielna przez 9, bo suma cyfr=1+2+4+2=9 dzieli się przez 9 bez reszty. Z podzielności przez 2 i przez 9 wynika podzielność liczby przez 18. 993312 jest podzielna przez 2, ponieważ ostatnia cyfra jest parzysta oraz jest podzielna przez 9, bo suma cyfr=9+9+3+3+1+2=27 dzieli się przez 9 bez reszty. Z podzielności przez 2 i przez 9 wynika podzielność liczby przez 18.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 20
Cecha podzielności przez 20: Ostatnia cyfra to 0, a przedostatnia cyfra jest parzysta.
Przykład: 1200 dzieli się przez 20, ponieważ ostatnia cyfra to 0, a przedostatnia cyfra jest parzysta. 13260 dzieli się przez 20, ponieważ ostatnia cyfra to 0, a przedostatnia cyfra jest parzysta.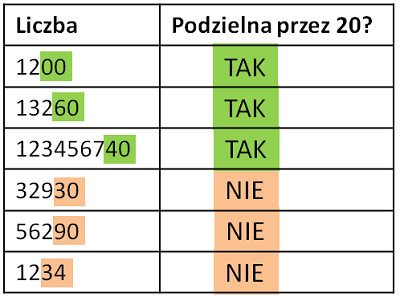
Przykład: 1200 dzieli się przez 20, ponieważ ostatnia cyfra to 0, a przedostatnia cyfra jest parzysta. 13260 dzieli się przez 20, ponieważ ostatnia cyfra to 0, a przedostatnia cyfra jest parzysta.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 21
Cecha podzielności przez 21:
Liczba spełnia jednocześnie cechę podzielności przez 3 i przez 7.

Liczba spełnia jednocześnie cechę podzielności przez 3 i przez 7.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 22
Cecha podzielności przez 22:
Liczba spełnia jednocześnie cechę podzielności przez 2 i przez 11.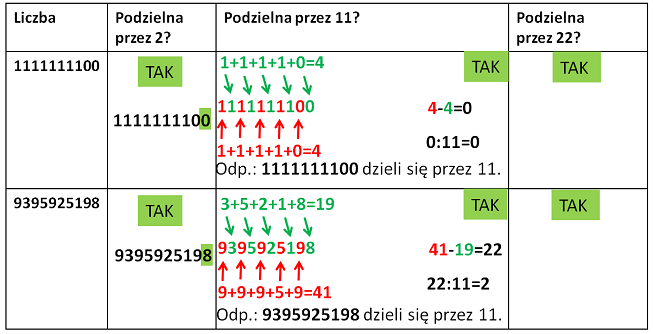
Liczba spełnia jednocześnie cechę podzielności przez 2 i przez 11.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 24
Cecha podzielności przez 24:
Liczba spełnia jednocześnie cechę podzielności przez 3 i przez 8.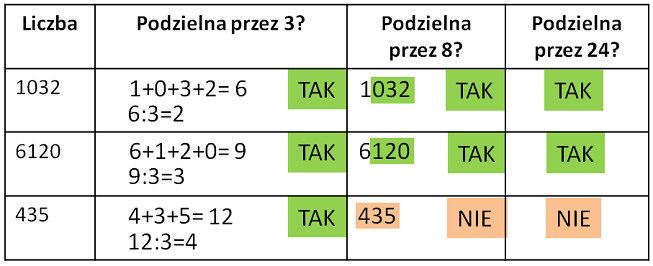
Liczba spełnia jednocześnie cechę podzielności przez 3 i przez 8.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 25
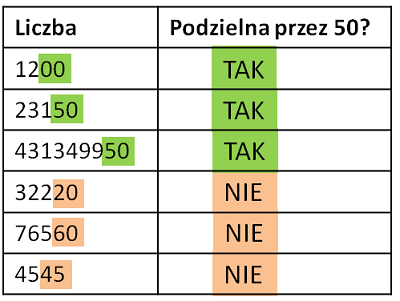
Cecha podzielności przez 25: ostatnie dwie cyfry to:00,25,50,75.
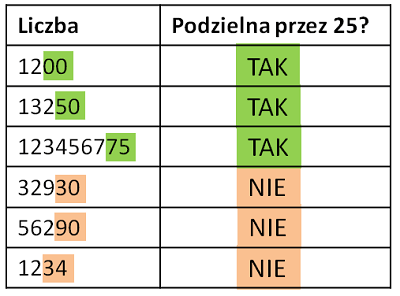

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 26
Cecha podzielności przez 26:
Liczba spełnia jednocześnie cechę podzielności przez 2 i przez 13.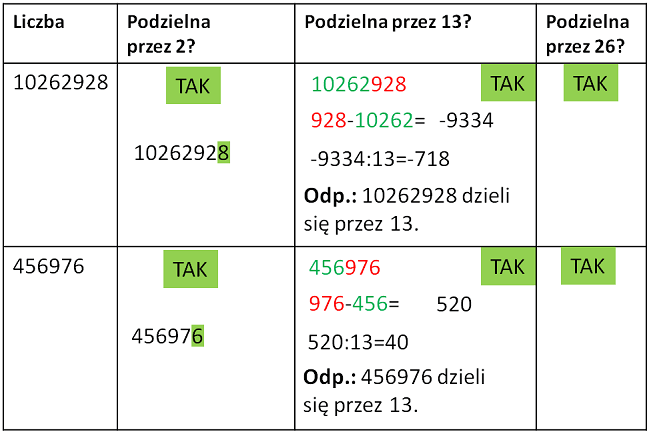
Liczba spełnia jednocześnie cechę podzielności przez 2 i przez 13.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 28
Cecha podzielności przez 28:
Liczba spełnia jednocześnie cechę podzielności przez 4 i przez 7.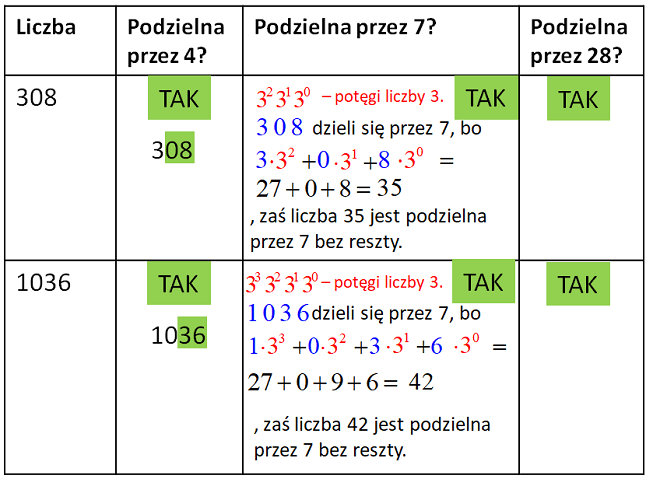
Liczba spełnia jednocześnie cechę podzielności przez 4 i przez 7.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 30
Cecha podzielności przez 30:
Liczba spełnia jednocześnie cechę podzielności przez 3 i przez 10.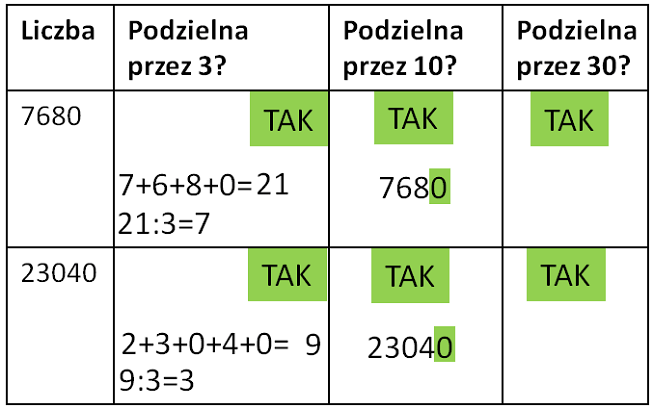
Liczba spełnia jednocześnie cechę podzielności przez 3 i przez 10.

Zobacz na stronie
Zobacz na YouTube
Cecha podzielności przez 50
Cecha podzielności przez 75
Cecha podzielności przez 75:
Liczba spełnia jednocześnie cechę podzielności przez 25 i przez 3.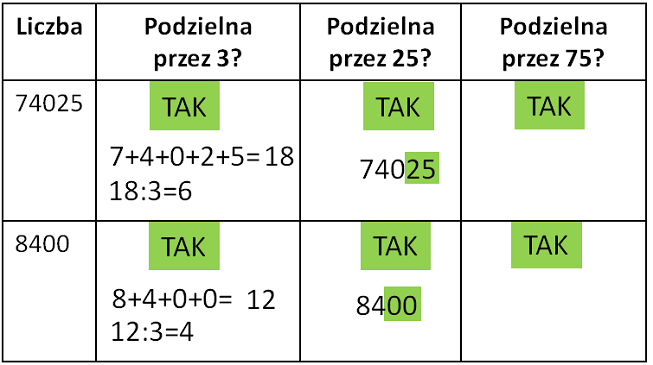
Liczba spełnia jednocześnie cechę podzielności przez 25 i przez 3.

Zobacz na stronie
Zobacz na YouTube
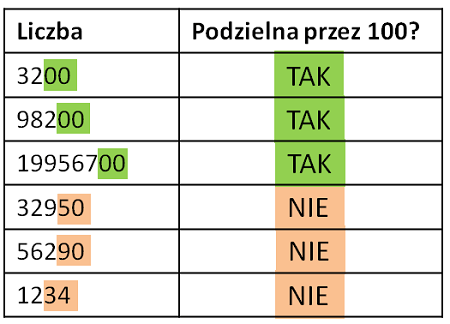
Cecha podzielności przez 100
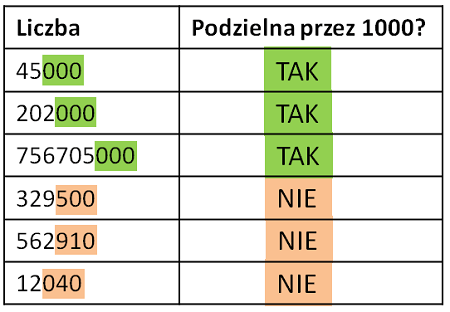
Cecha podzielności przez 1000
Cechy podzielności zadania
Zadanie.Liczba dzieli się przez 11, jeśli różnica między sumą cyfr stojących na miejscach parzystych (licząc od prawej), a sumą cyfr na miejscach
nieparzystych jest podzielna przez 11. Aby liczba \(394\left[ {} \right]0\left[ {} \right]8\) była podzielna przez 11, w puste miejsce można
wstawić:
A. 6 i 0. TAK/NIE
B. 8 i 9. TAK/NIE
C. 2 i 3. TAK/NIE
Zobacz na stronie
Zobacz na YouTube
Zadanie.Spośród 5 kolejnych liczb nieparzystych co najmniej jedna dzieli się zawsze przez:
A. 3, TAK/NIE
B. 5, TAK/NIE
C. 7, TAK/NIE
Zobacz na stronie
Zobacz na YouTube
Zadanie. Prawidłowo sformułowana cecha podzielności przez 4, to zdanie:
- Liczba jest podzielna przez 4, jeżeli jej dwie ostatnie cyfry są podzielne przez 4. PRAWDA/FAŁSZ
- Liczba jest podzielna przez 4, jeżeli jej dwie ostatnie cyfry tworzą liczbę podzielną przez 4. PRAWDA/FAŁSZ
- Liczba jest podzielna przez 4, jeżeli liczba jej setek jest podzielna przez 4. PRAWDA/FAŁSZ
Zobacz na stronie
Zobacz na YouTube
Cechy podzielności zadania trudniejsze
Zadanie. Jeżeli n jest liczbą naturalną podzielną przez 9, to każda liczba postaci
I. 2n jest podzielna przez 6 i 18. PRAWDA/FAŁSZ
II. n + 1 jest podzielna przez 10. PRAWDA/FAŁSZ
III. 3n – 1 jest liczbą nieparzystą. PRAWDA/FAŁSZ
Zobacz na stronie
Zobacz na YouTube
Zadanie. Znajdź liczbę wiedząc, że suma jej cyfr wynosi 6 i ma dokładnie 4 dzielniki, których suma wynosi 192. Odpowiedź uzasadnij.
Zobacz na stronie
Zobacz na YouTube
Zadanie. Wśród 10 kolejnych liczb naturalnych liczb podzielnych przez 3 może być:
A. 5, TAK/NIE
B. 4, TAK/NIE
C. 3, TAK/NIE
Zobacz na stronie
Zobacz na YouTube
Zadanie.
- Można wskazać taką liczbę czterocyfrową, podzielną przez 3, której wszystkie cyfry są podzielne przez 3. PRAWDA/FAŁSZ
- Każda liczba pięciocyfrowa podzielna przez 3 ma wszystkie cyfry podzielne przez 3. PRAWDA/FAŁSZ
- Istnieje taka liczba sześciocyfrowa podzielna przez 3, w której żadna cyfra nie jest podzielna przez 3. PRAWDA/FAŁSZ
Zobacz na stronie
Zobacz na YouTube
Zadanie Z cyfr 0, 2, 3, 4 utworzono wszystkie możliwe liczby czterocyfrowe, przy czym w poszczególnych liczbach każda z cyfr występuje tylko raz. Wśród tych liczb
I. Mamy do dyspozycji cyfry: 0,2,3,4. Zauważamy, że na początku nie może stać 0. Wobec tego mamy 3 możliwości zapełnienia pierwszego miejsca liczby 4-cyfrowej(2 lub 3 lub 4). Drugie miejsce można obstawić na 3 sposoby (dwie cyfry zostały z cyfr 2,3,4 oraz 0). Trzecie miejsce można zająć już na 2 sposoby, a ostatnie czwarte miejsce na 1 sposób. Łącznie takich liczb mamy: 3∙3∙2∙1=18. Odpowiedź: FAŁSZ.
II. Wiemy już, że jest 18 takich liczb 4-cyfrowych. Suma cyfr każdej z nich jest równa 3 zatem zgodnie z cechą podzielności liczb przez 3 wszystkie nasze liczby są podzielna przez 3. Odpowiedź: PRAWDA. Cecha podzielności przez 3 informuje nas, że liczba jest podzielna przez 3 wtedy, gdy suma cyfr dzieli się przez 3.
III. Aby liczba była podzielna przez 5 na końcu musi stać cyfra 0 lub 5. My mamy do dyspozycji cyfrę 0. Zatem ostatnie miejsce liczby 4-cyfrowej możemy uzupełnić na 1 sposób. Pierwsze miejsce liczby możemy uzupełnić na 3 możliwości, drugie miejsce na 2 sposoby, zaś przedostatnie miejsce na 1 sposób. Łącznie takich liczb mamy: 1∙3∙2∙1=6. Odpowiedź: PRAWDA.
- są 24 liczby podzielne przez 2. PRAWDA/FAŁSZ
- jest 18 liczb podzielnych przez 3. PRAWDA/FAŁSZ
- jest 6 liczb podzielnych przez 5. PRAWDA/FAŁSZ
Zobacz na stronie
Zobacz na YouTube
Rozwiązanie:I. Mamy do dyspozycji cyfry: 0,2,3,4. Zauważamy, że na początku nie może stać 0. Wobec tego mamy 3 możliwości zapełnienia pierwszego miejsca liczby 4-cyfrowej(2 lub 3 lub 4). Drugie miejsce można obstawić na 3 sposoby (dwie cyfry zostały z cyfr 2,3,4 oraz 0). Trzecie miejsce można zająć już na 2 sposoby, a ostatnie czwarte miejsce na 1 sposób. Łącznie takich liczb mamy: 3∙3∙2∙1=18. Odpowiedź: FAŁSZ.
II. Wiemy już, że jest 18 takich liczb 4-cyfrowych. Suma cyfr każdej z nich jest równa 3 zatem zgodnie z cechą podzielności liczb przez 3 wszystkie nasze liczby są podzielna przez 3. Odpowiedź: PRAWDA. Cecha podzielności przez 3 informuje nas, że liczba jest podzielna przez 3 wtedy, gdy suma cyfr dzieli się przez 3.
III. Aby liczba była podzielna przez 5 na końcu musi stać cyfra 0 lub 5. My mamy do dyspozycji cyfrę 0. Zatem ostatnie miejsce liczby 4-cyfrowej możemy uzupełnić na 1 sposób. Pierwsze miejsce liczby możemy uzupełnić na 3 możliwości, drugie miejsce na 2 sposoby, zaś przedostatnie miejsce na 1 sposób. Łącznie takich liczb mamy: 1∙3∙2∙1=6. Odpowiedź: PRAWDA.
Cechy podzielności zadania bardzo trudne
Zadanie. Przez 11 jest podzielna liczba
- \({10^4} – {1^4}\) PRAWDA/FAŁSZ
- \({10^{99}} + {1^{99}}\) PRAWDA/FAŁSZ
- \({10^{200}} + {1^{200}}\) PRAWDA/FAŁSZ
Zobacz na stronie
Zobacz na YouTube
Zadanie. Udowodnij, że jeżeli liczba całkowita m przy dzieleniu przez 7 daje resztę 4, a liczba całkowita n przy dzieleniu przez 7 daje resztę 3, to iloczyn mn przy dzieleniu przez 7 daje resztę 5.
Zobacz na stronie
Zobacz na YouTube
Zadanie. Uzasadnij, że dla n naturalnego każda liczba postaci 2n+2n+1+2n+2+2n+3 jest podzielna przez 5.
Zobacz na stronie
Zobacz na YouTube
Zadanie. W torebce jest mniej niż 100 cukierków. Wiadomo, że można je podzielić na 5 równych części oraz można je podzielić na 6 równych części. Natomiast, gdyby próbować je podzielić na 7 równych części, to zabraknie trzech cukierków. Oblicz, ile jest tych cukierków?
Zobacz na stronie
Zobacz na YouTube
Zadanie. Wykaż, że liczba \({36^{51}} + {9^{50}} – {6^{100}} + {3^{102}}\) jest podzielna przez 5.
Zobacz na stronie
Zobacz na YouTube
Zadanie. Liczbą naturalną jest
- \(\frac{{{10}^{85}}+2}{6}\) PRAWDA/FAŁSZ
- \(\frac{{{5}^{127}}+1}{2}\) PRAWDA/FAŁSZ
- \(\frac{{{10}^{999}}-1}{9}\) PRAWDA/FAŁSZ
Zobacz na stronie
Zobacz na YouTube
Uwaga: Sprawdź, czy licznik ułamka jest podzielny odpowiednio przez 6, 2, 9.
Zadanie. Dana jest liczba 1092-92. Prawdą jest, że:
A. Suma cyfr tej liczby wynosi 818. TAK/NIE
B. Liczba ta jest podzielna przez 4. TAK/NIE
C. Liczba ta jest podzielna przez 8. TAK/NIE
Zobacz na stronie
Zobacz na YouTube
Zadanie. Liczba n(n+1)(n+2)(n+3) dla dowolnego naturalnego dzieli się przez:
A. 12, TAK/NIE
B. 24, TAK/NIE
C. 36, TAK/NIE
Zobacz na stronie
Zobacz na YouTube
Zadanie. Uzasadnij, że liczba a=92015+2015 jest podzielna przez 2.
Zobacz na stronie
Zobacz na YouTube
Zadanie. Wykaż, że liczba \({{3}^{22}}+{{6}^{21}}\) jest podzielna przez 5.
Zobacz na stronie
Zobacz na YouTube
Zadanie. Uzasadnij, że iloczyn liczb: \(1\cdot 3\cdot 5\cdot 7\cdot …\cdot 2007\cdot 2009\cdot 2011\) jest podzielny przez 2013.
Zobacz na stronie
Zobacz na YouTube
Zadanie. Różnica kwadratów dwóch
- kolejnych liczb całkowitych jest liczbą nieparzystą. PRAWDA/FAŁSZ
- kolejnych liczb naturalnych nieparzystych jest podzielna przez 8. PRAWDA/FAŁSZ
- liczb całkowitych różniących się o 2 jest liczbą podzielną przez 4. PRAWDA/FAŁSZ
Zobacz na stronie
Zobacz na YouTube
Zadanie.
- Jeżeli wszystkie cyfry liczby czterocyfrowej są podzielne przez 3, to liczba ta jest podzielna przez 3. PRAWDA/FAŁSZ
- Każda liczba trzycyfrowa podzielna przez 3 ma wszystkie cyfry podzielne przez 3. PRAWDA/FAŁSZ
- Suma kwadratów trzech kolejnych liczb naturalnych \(\underline{nie}\) dzieli się przez 3. PRAWDA/FAŁSZ
Zobacz na stronie
Zobacz na YouTube
Cechy podzielności liczb są niezwykle ważne w matematyce i innych dziedzinach nauki. Pozwalają one na rozwiązywanie problemów związanych z matematycznymi właściwościami liczb oraz są kluczowe w kryptografii, gdzie bezpieczeństwo wielu algorytmów opiera się na trudności w rozkładaniu dużych liczb na czynniki pierwsze. Dlatego też zrozumienie tych cech jest istotne dla każdego, kto zajmuje się matematyką i naukami przyrodniczymi.
Bądź na bieżąco z MatFiz24.pl