Konkurs kuratoryjny z matematyki 2015/16 – Śląskie – Etap wojewódzki
KONKURS PRZEDMIOTOWY Z MATEMATYKI, ETAP WOJEWÓDZKI
Informacje dla ucznia:
- Na stronie tytułowej arkusza w wyznaczonym miejscu wpisz swój kod ustalony przez komisję.
- Sprawdź, czy arkusz konkursowy zawiera 8 stron (zadania 1-13).
- Czytaj uważnie wszystkie teksty i zadania.
- Rozwiązania zapisuj długopisem lub piórem. Nie używaj korektora.
- Staraj się nie popełniać błędów przy zaznaczaniu odpowiedzi, ale jeśli się pomylisz, błędne zaznaczenie otocz kółkiem ⊗ i zaznacz inną odpowiedź znakiem „X”.
- W zadaniach typu PRAWDA/FAŁSZ oceń, czy podane zdania są prawdziwe, czy fałszywe. Zaznacz właściwą odpowiedź.
- Rozwiązania zadań otwartych zapisz czytelnie w wyznaczonych miejscach. Pomyłki przekreślaj.
- Przygotowując odpowiedzi na pytania, możesz skorzystać z miejsc opatrzonych napisem Brudnopis. Zapisy w brudnopisie nie będą sprawdzane i oceniane.
- Podczas rozwiązywania zadań nie wolno Ci korzystać z kalkulatora.
- Czas pracy: 120 minut
Plik z zadaniami z konkursu kuratoryjnego – etap wojewódzki
Pobierz zadania matematyczne z konkursu tutaj.
I część konkursu kuratoryjnego z matematyki – etap wojewódzki
Rozwiąż krzyżówkę. Hasło w zacieniowanych kratkach, to miejsce spotkań znanych polskich matematyków okresu międzywojennego. Hasło nie jest oceniane, ale może zweryfikować Twoje odpowiedzi.
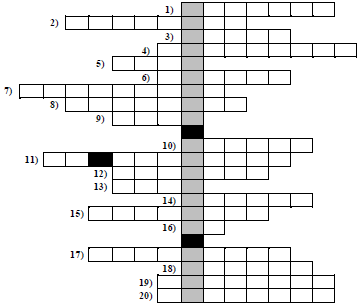
- Czworokąt posiadający 4 osie symetrii.
- Jeden z dwóch równoległych boków trapezu.
- Bryła obrotowa powstała na skutek obrotu prostokąta wokół jednego z jego boków.
- Liczba 8 w ułamku, który powstaje po skróceniu liczby 0,125 zapisanej w postaci ułamka zwykłego.
- Bryła, która powstaje w wyniku obrotu koła wokół jego średnicy.
- Jeden z dwóch wielokątów, które powstają po przecięciu trójkąta prostą równoległą do jego podstawy, nieprzechodzącą przez wierzchołek tego trójkąta.
- W kwadracie o boku \(a\sqrt{10}\) długość tego odcinka wynosi \(2a\sqrt{5}\)
- Najdłuższa cięciwa okręgu.
- Milion gramów.
- Bryła obrotowa, której objętość stanowi 1/3 objętości walca o takiej samej podstawie i wysokości.
- Prosta, której każdy punkt odpowiada pewnej liczbie rzeczywistej.
- Przyporządkowanie każdemu elementowi jednego zbioru dokładnie jednego elementu drugiego zbioru.
- Średnia arytmetyczna dwóch liczb przeciwnych.
- Słownie wynik dzielenia liczby XL przez X.
- Stosunek drogi do czasu w ruchu jednostajnym.
- 0,01 hektara.
- Działanie zapisywane w postaci ułamka.
- Geometryczna interpretacja funkcji.
- Równość dwóch wyrażeń algebraicznych.
- Odcinek łączący wierzchołek stożka z punktem na okręgu jego podstawy.
W zadaniach od 2. do 9. oceń, czy podane zdania są prawdziwe, czy fałszywe. Zaznacz właściwą odpowiedź.
W trójkąt prostokątny ABC wpisano okrąg o środku S. Kąt CAB tego trójkąta jest kątem prostym.
S(n) oznacza sumę cyfr liczby naturalnej n.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Spośród 24 uczniów pewnej klasy 16 lubi pływać, 18 lubi słuchać muzyki, a 20 lubi jeździć na rowerze. Jest co najwyżej
Jeżeli n jest liczbą naturalną podzielną przez 9, to każda liczba postaci
W pewnym trójkącie jeden z boków ma długość \(8+8\sqrt{3}\) , a kąty do niego przyległe mają miary 45° i 30°.
Równanie (m-3n+1)x-2m+4n-1=0
Stożek S przecięto w połowie jego wysokości płaszczyzną równoległą do podstawy. Otrzymano w ten sposób dwie nowe bryły, w tym stożek S’.
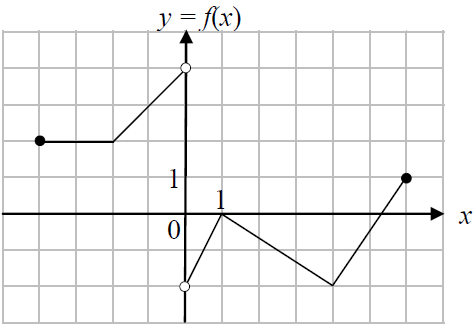
Na rysunku przedstawiono wykres funkcji f.
Środkowa trójkąta, to odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku. Środkowe przecinają się w jednym punkcie, który dzieli każdą z nich w stosunku 2:1, licząc od wierzchołka trójkąta. Oblicz długości środkowych trójkąta o bokach długości: 10, 10, 12.
Treść dostępna po opłaceniu abonamentu.W dwóch urnach znajdują się kule białe i czarne. W pierwszej urnie jest 15 kul, w tym 5 białych, w drugiej – 25 kul, w tym 18 czarnych. Do obu urn należy dołożyć w sumie 16 białych kul. Oblicz, po ile kul należy dołożyć do każdej urny, aby prawdopodobieństwa wylosowania kuli białej z każdej nich były równe?
Treść dostępna po opłaceniu abonamentu.Do sklepu dostarczono 18 skrzynek z owocami. W każdej skrzynce była taka sama liczba owoców. Z części skrzynek sprzedano połowę owoców, z części \(\frac{1}{3}\), a w części skrzynek pozostały wszystkie owoce. W sumie sprzedano \(\frac{1}{9}\) liczby dostarczonych owoców. Oblicz, w ilu skrzynkach pozostały wszystkie owoce.
Treść dostępna po opłaceniu abonamentu.Dany jest trójkąt równoramienny ABC o podstawie AB i kącie przy podstawie równym 50°. Wewnątrz trójkąta obrano punkt K taki, że |∠KAB|=30° i |∠KBA|=10°. Na półprostej AK wybrano taki punkt L, że |∠ABL|=30°. Uzasadnij, że trójkąty BCL i BKL są przystające.
Treść dostępna po opłaceniu abonamentu.



