Konkurs kuratoryjny z matematyki 2007/08 – Śląskie – Etap szkolny
KONKURS PRZEDMIOTOWY Z MATEMATYKI, ETAP SZKOLNY – 8 listopada 2007 r.
Przeczytaj uważnie poniższą instrukcję:
- Test składa się z 14 zadań.
- Przy numerze każdego zadania została podana maksymalna liczba punktów możliwych do zdobycia za to zadanie.
- Przeczytaj dokładnie treść zadań, zwracając uwagę na to, czy polecenie nakazuje podać jedynie wynik, czy też obliczyć szukaną wielkość (tzn. zapisać obliczenie) lub w inny sposób uzasadnić odpowiedź.
- W części I (zadania od 1 do 9) wpisz TAK lub NIE obok każdej z trzech odpowiedzi. Za każdy poprawny wpis otrzymasz 1 punkt – w sumie za każde z tych zadań możesz otrzymać maksymalnie 3 punkty.
- Margines po prawej stronie kartki jest przeznaczony na brudnopis.
- Na rozwiązanie wszystkich zadań masz 90 minut.
- Aby zakwalifikować się do etapu rejonowego musisz zdobyć co najmniej 39 punktów.
Plik z zadaniami z konkursu kuratoryjnego – etap szkolny
Pobierz zadania z konkursu tutaj.
I część konkursu kuratoryjnego z matematyki – etap szkolny
Jeżeli długości dwóch boków trójkąta wynoszą 3 m i 6 m, to długość trzeciego boku będąca liczbą całkowitą:
Trzy różne proste mogą podzielić płaszczyznę na:
W układzie współrzędnych punkty przecięcia prostych: x = 2, x = -2, y = 3, y = -3 wyznaczają wierzchołki prostokąta. Prawdziwe jest zdanie:
Dwaj podróżnicy wyruszają jednocześnie z miasta: jeden na wschód, drugi na północ. Jeden z nich przebywa dziennie 40 km, drugi 50 km. Odległość między nimi będzie mniejsza niż 600 km:
Jeżeli 4 pracowników przygotowuje 500 przesyłek w ciągu 2 godzin to:
Cukiernik obliczył, że wypieczone przez niego ciasto waży o 25 % więcej niż wzięta do wypieku mąka. Wynika z tego, że:
Dwusieczne kątów przy dolnej podstawie trapezu przecinają się w punkcie leżącym na górnej podstawie. Wtedy zawsze:
Średnia wieku 27 osobowej grupy dzieci jest równa 14 lat. Gdy obliczymy średnią wieku uczniów razem z opiekunem, to średnia wyniesie 15 lat. Wynika z tego, że:
Wartość wyrażenia (x+1)2-(2x+0,5)2 wynosi 0 dla:
II część konkursu kuratoryjnego z matematyki – zadania otwarte
Oblicz miarę kąta wewnętrznego w 12-kącie foremnym.
Sprawdź, że jeżeli: \(\frac{a+b}{c}=\frac{a+c}{b}=1\) (b ≠ 0 i c ≠ 0) to a=0 i b=c.
Sprawdź , że \(\sqrt{2}=1+\frac{1}{2+\frac{1}{1+\sqrt{2}}}\)
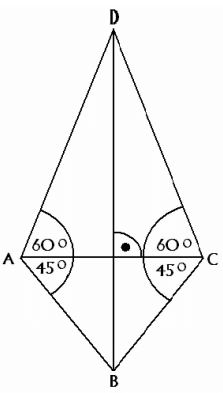
Maciek chce zbudować latawiec w kształcie deltoidu przedstawionego na rysunku. Z listewek zbuduje szkielet latawca składający się z boków oraz przekątnych tego czworokąta. Wiedząc, że AC = 40 cm, oblicz, ile co najmniej metrów listewek Maciek musi zakupić. Wynik podaj z dokładnością do 0,01m, przyjmując z nadmiarem, że: \(\sqrt{2}\approx 1,42\,,\quad a\quad \sqrt{3}\approx 1,74.\)
Właśnie teraz wychodzę. Jeżeli pójdę z prędkością 6 km/h, to dojdę do celu o godzinie 12.00, a jeżeli z prędkością 5 km/h, to dojdę o godzinie 12.30. Oblicz, jak daleko jest do celu oraz która jest teraz godzina.




