Konkurs kuratoryjny z matematyki 2004/2005 – Śląskie – Etap wojewódzki
Konkurs przedmiotowy z matematyki – Finał wojewódzki – 16 marca 2005 r.
Przeczytaj uważnie poniższą instrukcję:
- Test składa się z 15 zadań. Przy numerze każdego zadania została podana maksymalna liczba punktów możliwych do zdobycia za to zadanie.
- Przeczytaj uważnie treść zadań. Odpowiedzi do zadań w części I zaznacz w tabeli. Pozostałe rozwiązania wpisz na oddzielne kartki.
- Na rozwiązanie wszystkich zadań masz 90 minut.
Plik z zadaniami konkursu kuratoryjnego do pobrania
Plik do ściągnięcia znajdziesz tutaj.
Część I konkursu kuratoryjnego
Różna od 1 jest liczba:
Połowa liczby 298 wynosi:
Gra polega na podwójnym rzucie sześcienną kostką do gry. Gracz wygrywa, gdy w obu rzutach otrzyma sumę oczek większą od 9. Ile wynosi szansa wygranej?
Każda liczba rzeczywista spełnia nierówność:
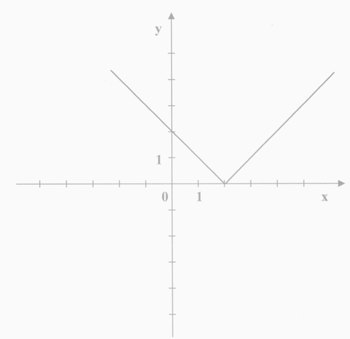
Funkcja, której wykres przedstawiony jest na rysunku obok, wyraża się wzorem:
Jeżeli w pewnym trójkącie jedna ze środkowych jest wysokością, to ten trójkąt na pewno jest:
Przekątna kwadratu ma długość \(5\sqrt{2}\)cm. Pole tego kwadratu wynosi:
Dwa ostrosłupy mają przystające podstawy i objętości równe odpowiednio 12cm3 i 96cm3. Jeżeli wysokość pierwszego ostrosłupa ma długość 3 cm, to wysokość drugiego wynosi:
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
O godzinie 930 wskazówki zegara utworzą kąt:
Jeżeli 4 myszy zjadają 4 kilogramy sera w ciągu 4 minut, to 60 myszy zje 60 kg sera w ciągu:
Część II konkursu kuratoryjnego – zadania otwarte
Różnica dwóch liczb jest równa 2, a różnica kwadratów tych liczb wynosi 100. Znajdź te liczby.
Treść dostępna po opłaceniu abonamentu.Asi zerwał się naszyjnik. Trzecią część korali znalazła na podłodze, jedna czwartą w kieszeni, jedną piątą pod oparcie kanapy, a szósta część korali została na sznurku. Sześciu korali nie udało się jej znaleźć. Oblicz, ile korali zostało na sznurku?
Treść dostępna po opłaceniu abonamentu.W torebce jest mniej niż 100 cukierków. Wiadomo, że można je podzielić na 5 równych części oraz można je podzielić na 6 równych części. Natomiast, gdyby próbować je podzielić na 7 równych części, to zabraknie trzech cukierków. Oblicz, ile jest tych cukierków?
Treść dostępna po opłaceniu abonamentu.Oblicz pole zacieniowanej figury przedstawionej na rysunku obok, będącej częścią kwadratu o boku długości 1. Przyjmij, że białe półkola są przystające i styczne.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Basen olimpijski ma 50 m długości. W jednym końcu basenu głębokość jest równa 1,5 m, a w drugim 3 m. Oblicz głębokość basenu w odległości 10 m od płytszego końca basenu. Kąt nachylenia dna do powierzchni wody jest stały. Wykonaj rysunek pomocniczy.
Treść dostępna po opłaceniu abonamentu.



