Konkurs kuratoryjny z matematyki 2011/12 – Śląskie – Etap szkolny
Zobacz wszystkie zadania i rozwiązania w postaci wideo konkursu kuratoryjnego z matematyki 2011 / 2012 województwa śląskiego – etap szkolny gimnazjum.
Rozwiąż krzyżówkę. Hasło krzyżówki nie jest oceniane, ale zweryfikuje Twoje odpowiedzi. Odczytasz je w zacieniowanych okienkach.
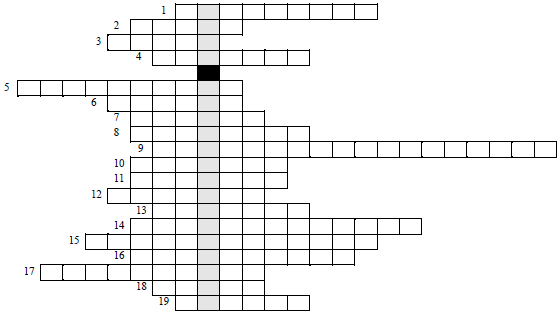
1. Dodawane do siebie liczby.
2. Można go wykreślić za pomocą cyrkla.
3. Jeden wspólny dla dwóch prostych przecinających się.
4. Prosta, która ma z okręgiem dokładnie jeden punkt wspólny.
5. Półprosta, która dzieli kąt na połowy.
6. Wynik dzielenia liczb.
7. Czworokąt, który ma co najmniej jedną parę boków równoległych.
8. Liczba naturalna, większa od jedności, podzielna przez 1 i samą siebie.
9. Najdłuższy bok w trójkącie prostokątnym.
10. Liczba, od której odejmujemy.
11. Odcinek łączący środek okręgu z punktem na okręgu.
12. Odcinek łączący dwa punkty na okręgu.
13. Prostokąt, który ma wszystkie boki równej długości.
14. Trójkąt, który ma co najmniej dwa boki równej długości.
15. Czworokąt, który ma dwie pary boków równoległych.
16. Prosta prostopadła do odcinka i dzieląca go na połowy.
17. Proste na płaszczyźnie, które nie mają punktów wspólnych.
18. Kąt o mierze 360°.
19. 10 000 m² to … .
Dla liczb x = 0 i x = -1 traci sens liczbowy wyrażenie
- \(1+\frac{1}{1+\frac{1}{x}}\) PRAWDA/FAŁSZ
- \(\frac{3}{\left( x-1 \right)} \) PRAWDA/FAŁSZ
- \(\sqrt{x}-\frac{1}{x}\) PRAWDA/FAŁSZ
Wartość zero przyjmuje wyrażenie arytmetyczne
- \(\pi -3,14\) PRAWDA/FAŁSZ
- \(5\sqrt{2}-\sqrt{50}\) PRAWDA/FAŁSZ
- \({{\left( \frac{2\sqrt{7+4}}{\sqrt{2}} \right)}^{0}}-1\) PRAWDA/FAŁSZ
Cena towaru wzrosła o 25%. Jeśli oznaczymy przez x cenę po podwyżce, to cenę przed podwyżką można zapisać jako
- 0,75x PRAWDA/FAŁSZ
- x – 20% PRAWDA/FAŁSZ
- \(x-\frac{1}{5}x\) PRAWDA/FAŁSZ
W dwóch kwintalach zboża jest 2% zanieczyszczeń. (1 kwintal = 100 kg)
- W jednym kwintalu tego zboża jest 1% zanieczyszczeń. PRAWDA/FAŁSZ
- W czterech kwintalach tego zboża jest 8 kg zanieczyszczeń. PRAWDA/FAŁSZ
- W ośmiu kwintalach tego zboża jest 4% zanieczyszczeń. PRAWDA/FAŁSZ
Liczby a, b i c określone są następująco:
\(a={{3}^{10}}+{{3}^{10}}+{{3}^{10}},\quad b={{3}^{30}}\cdot {{3}^{2}},\quad c={{\left( {{3}^{15}} \right)}^{2}}.\)
Zatem
- a = c PRAWDA/FAŁSZ
- b \(\le \) c PRAWDA/FAŁSZ
- a < b PRAWDA/FAŁSZ
Woda zmieniając się w lód zwiększa objętość o \(\frac{1}{11}\). Zatem
- 1 dm³ lodu po roztopieniu daje \(\frac{11}{12} \)dm³ wody. PRAWDA/FAŁSZ
- z 2 litrów lodu uzyska się \(1\frac{5}{6} \) litra wody. PRAWDA/FAŁSZ
- objętość lodu po roztopieniu zmniejszy się o \(\frac{1}{12} \). PRAWDA/FAŁSZ
Dany jest okrąg o środku O i promieniu 10, a prosta AB jest styczna do niego w punkcie B. Kąt OAB ma miarę 30°.
- \(\left| OA \right|=20\) PRAWDA/FAŁSZ
- Pole trójkąta OBA jest równe \(50\sqrt{3}\). PRAWDA/FAŁSZ
- Jeżeli punkt C jest punktem wspólnym odcinka OA z okręgiem, to łuk CB zawarty w trójkącie OAB ma długość równą \(5\pi \). PRAWDA/FAŁSZ
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Jeśli wysokość trójkąta równobocznego ma długość 6, to
- bok tego trójkąta ma długość \(6\sqrt{3}\). PRAWDA/FAŁSZ
- pole tego trójkąta wynosi 12. PRAWDA/FAŁSZ
- promień okręgu opisanego na tym trójkącie ma długość 4. PRAWDA/FAŁSZ
Wykaż, że liczba \({{3}^{22}}+{{6}^{21}}\) jest podzielna przez 5.
Treść dostępna po opłaceniu abonamentu.Podstawy trapezu równoramiennego mają długości 7 cm i 14 cm. Przekątna trapezu zawiera się w dwusiecznej kąta przy dłuższej podstawie. Oblicz obwód i pole tego trapezu.
Treść dostępna po opłaceniu abonamentu.Ewa i Marek wyruszyli z domu jednocześnie na pieszą wycieczkę tą samą trasą. Marek szedł ze stałą prędkością 6 km/h, a po 2 godzinach i 15 minutach zatrzymał się. Odpoczywał 25 minut, po czym wyruszył w drogę powrotną. Szedł nadal ze stałą prędkością 6 km/h. Ewa utrzymywała stałą prędkość marszu 4 km/h aż do spotkania z Markiem, a następnie wrócili razem do domu. Oblicz, po jakim czasie Ewa spotkała się z Markiem. Wyznacz drogę, jaką przeszła Ewa do momentu spotkania z Markiem. Oblicz, jaką drogę pokonał Marek w czasie całej wycieczki.
Odp.:
Ewa spotkała się z Markiem po upływie …………………………….
Ewa do spotkania z Markiem pokonała drogę …………………………….
Marek w czasie całej wycieczki pokonał drogę …………………………….
Prostokątną działkę o obwodzie 280 m podzielono na 4 działki o jednakowych wymiarach (jak na rysunku). Oblicz pole tej działki. Wynik podaj w hektarach.
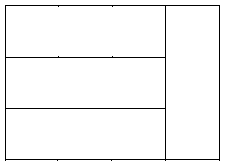 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.




