Egzamin ósmoklasisty z matematyki 2019 CKE – dodatkowy – czerwiec

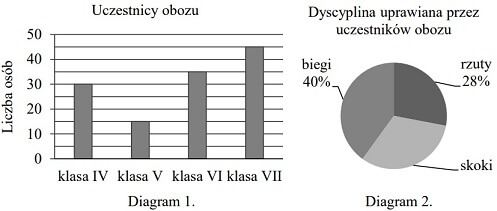
Na obozie sportowym przebywali uczniowie z klas IV, V, VI i VII. Liczbę uczestników obozu z poszczególnych klas przedstawiono na diagramie 1.
Każdy z uczestników obozu uprawia jedną z trzech dyscyplin lekkoatletycznych: biegi, rzuty, skoki. Na diagramie 2. przedstawiono, jaka część uczniów trenuje poszczególne dyscypliny.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wśród wszystkich uczestników obozu 28% stanowili uczniowie z klas

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

Skoki trenuje więcej osób niż rzuty. P/F
Biegi trenuje o 10 osób więcej niż skoki. P/F

Podczas lekcji matematyki uczniowie zaokrąglali liczbę 0,84631. Adam zaokrąglił tę liczbę do części dziesiątych, Bartek – do części setnych, Magda – do części tysięcznych, a Zosia – do części dziesięciotysięcznych.

Które z dzieci otrzymało największą liczbę? Wybierz właściwą odpowiedź spośród podanych.

Rowerzysta wyruszył w trasę o godzinie \({{10}^{45}}\) , a do celu przyjechał o godzinie 1405. Jego prędkość średnia na całej trasie była równa \(15\frac{km}{h}.\)

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wyrażenie: (x − 2)(4x − 3) − x(1− x) po uproszczeniu jest równe

Na rysunku przedstawiono kształt i wymiary elementu układanki, w którym sąsiednie boki są do siebie prostopadłe

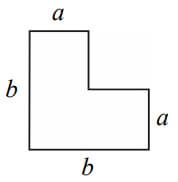
Z takich elementów zbudowano dwie figury przedstawione na poniższym rysunku

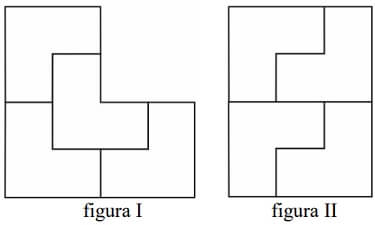
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

Obwód figury I jest o 2b większy od obwodu figury II. P/F
Pole figury II jest równe \(12{{a}^{2}}\). P/F

Wydajność dużej pompy strażackiej to 24 000 litrów wody na minutę, natomiast wydajność małej pompy to 1200 litrów wody na minutę. Mała pompa w ciągu 1 godziny pracy zużywa 0,931 litra paliwa.

Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.

W ciągu jednej godziny działania dużej pompy strażackiej przepłynie przez nią A/B litrów wody niż w tym samym czasie przez małą pompę.

Mała pompa w ciągu 15 godzin pracy zużyj C/D litrów paliwa.

Na poniższej osi liczbowej literami k, l, m, n oznaczono cztery kolejne liczby całkowite. Jedna z tych liczb jest równa 0. Kropką oznaczono liczbę \(\sqrt{41}\) .

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Na osi liczbowej liczbę 0 oznaczono literą

Dane są punkty o współrzędnych: A = (2, 1), B = (4, 9), C = (–2, 5), D = (8, 5).

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe

Środek odcinka AB ma współrzędne (3, 5). P/F
Środek odcinka AB jest także środkiem odcinka CD. P/F

W prostokątnym układzie współrzędnych zaznaczono wierzchołki trójkąta prostokątnego ABC (patrz: rysunek).

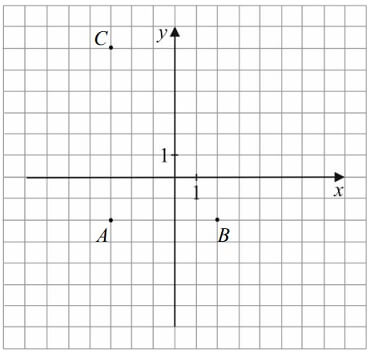
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Przeciwprostokątna trójkąta ABC ma długość

Rzucono czterema symetrycznymi sześciennymi kostkami do gry. Na 20 widocznych ścianach tych czterech kostek suma oczek jest równa 76. Za niewidoczną uznano ścianę, na której kostka stoi.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

Na każdej z niewidocznych ścian tych kostek jest jedno oczko. P/F
Na niewidocznej ścianie jednej z tych kostek może być pięć oczek. P/F

Na rysunku przedstawiono dwa trójkąty oraz podano niektóre ich wymiary i miary kilku kątów.

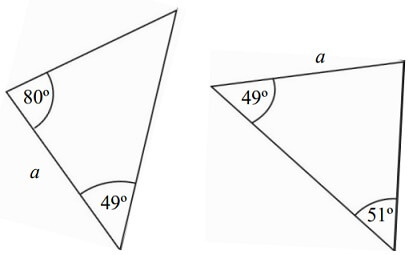
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

Te trójkąty są równoramienne. P/F
Te trójkąty są przystające. P/F

W trójkącie ABC, w którym |AC| = |BC| , poprowadzono wysokość CD. Obwód trójkąta ACD jest równy 24 cm, a obwód trójkąta ABC jest równy 36 cm.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

Obwód trójkąta BCD jest równy 18 cm. P/F
Wysokość CD ma długość 6 cm. P/F

Na rysunku przedstawiono fragment siatki prostopadłościanu oraz podano długości niektórych jego krawędzi.

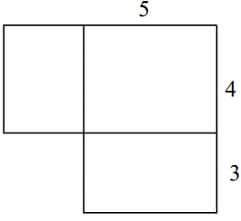
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Suma długości wszystkich krawędzi prostopadłościanu jest równa

Z sześciu jednakowych sześciennych klocków o krawędzi 1 cm zbudowano bryłę I. Następnie z bryły tej usunięto dwa sześciany i otrzymano bryłę II (patrz: rysunki).

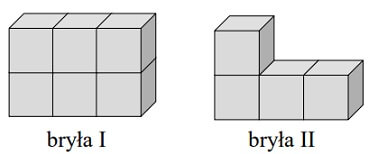
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Pole powierzchni bryły II jest mniejsze od pola powierzchni bryły I o

We wtorek w kwiaciarni obowiązywały ceny zapisane poniżej.

Za dodatki użyte do wykonania bukietu dolicza się 20% wartości kwiatów, z których wykonano ten bukiet. Ile zapłaci tego dnia klient za bukiet złożony z 3 tulipanów, 2 róż i 5 goździków? Zapisz obliczenia

Pan Jan wybrał z bankomatu 2900 zł. Na tę kwotę składały się łącznie 22 banknoty 200-złotowe i 100-złotowe. Ile banknotów 100-złotowych pan Jan wybrał z bankomatu? Zapisz obliczenia.

W trójkącie równoramiennym ABC, w którym |AC|=| BC|, poprowadzono dwie wysokości: AD i CE. Na rysunku przedstawiono ten trójkąt i zaznaczono w nim niektóre kąty.

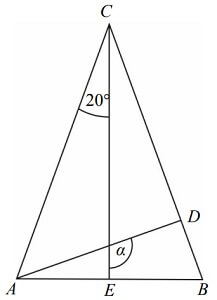
Uzasadnij, że kąt α ma miarę 110°.

Bilet normalny na koncert kosztuje 45 zł, a cena biletu ulgowego stanowi \(\frac{5}{9}\) ceny biletu normalnego. Janek zakupił pięć razy więcej biletów normalnych niż biletów ulgowych. Za wszystkie bilety zapłacił 500 zł. Ile biletów każdego rodzaju Janek zakupił? Zapisz obliczenia.

Duży prostokąt przedstawiony na rysunku jest podzielony na osiem małych przystających prostokątów.

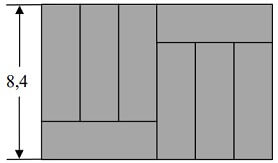
Oblicz obwód dużego prostokąta. Zapisz obliczenia.

Przedstawione na rysunku trójkąt prostokątny równoramienny oraz kwadrat mają równe pola.

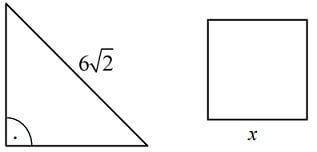
Oblicz obwód kwadratu. Zapisz obliczenia.