Egzamin ósmoklasisty z matematyki 2020 CKE
Zadania z egzaminu ósmoklasisty 2020 matematyka
Egzamin ósmoklasisty 2020 matematyka – zadania testowe
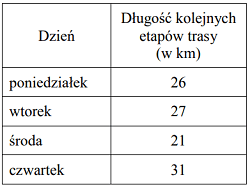
Rowerzysta uczestniczył w rajdzie rowerowym. Całą trasę rajdu pokonał w ciągu czterech dni. W tabeli poniżej przedstawiono długości kolejnych etapów trasy, które przebył każdego dnia.
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
W poniedziałek i wtorek rowerzysta przejechał łącznie A/B długości całej trasy rajdu
W środę rowerzysta przejechał C/D długości całej trasy rajdu
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych
Wartość wyrażenia \(\frac{5}{7}-\frac{2}{7}\cdot \left( -\frac{3}{2} \right)\) jest równa
Trzej właściciele firmy – Adam, Janusz i Oskar – kupili samochód dostawczy za kwotę 154 000 zł. Kwoty wpłacone przez Adama, Janusza i Oskara są – odpowiednio – w stosunku 2 : 3 : 6.
Jaką kwotę wpłacił Janusz? Wybierz właściwą odpowiedź spośród podanych.
Na przedstawionym poniżej fragmencie osi liczbowej oznaczono cztery punkty: R, S, T, W. Współrzędne punktów S i W są równe 287 i 311. Odcinek RW jest podzielony na pięć równych części.
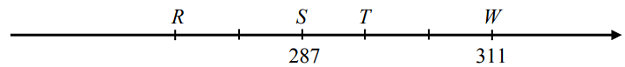
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Współrzędne punktów R i T różnią się o 24. P/F
Współrzędna punktu R jest równa 271. P/F
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Pociąg o długości l = 150 m przejechał przez tunel o długości d = 350 m ze stałą prędkością \(V=20\frac{m}{s}.\)
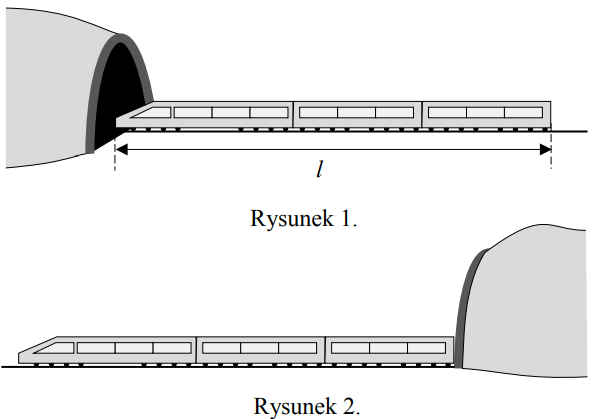
Ile czasu upłynęło od momentu wjazdu czoła pociągu do tunelu (rysunek 1.) do momentu wyjazdu z tunelu końca ostatniego wagonu (rysunek 2.)? Wybierz właściwą odpowiedź spośród podanych.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość wyrażenia \(\sqrt{3}\left( \sqrt{27}-\sqrt{12} \right)\) jest równa
Która z podanych niżej liczb nie jest równa \({{3}^{15}}\)? Wybierz właściwą odpowiedź spośród podanych.
Na diagramie przedstawiono wyniki (w centymetrach) uzyskane przez zawodników uczestniczących w finale konkursu skoku wzwyż.
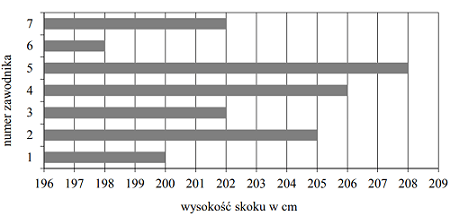
Ilu zawodników uzyskało wynik wyższy od średniej arytmetycznej wyników wszystkich uczestników finału tego konkursu? Wybierz właściwą odpowiedź spośród podanych.
Na kartonowej siatce sześcianu Mariusz nakleił 6 figur tak, jak pokazano na rysunku. Następnie z tej siatki skleił kostkę.
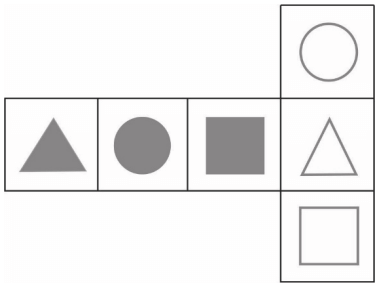
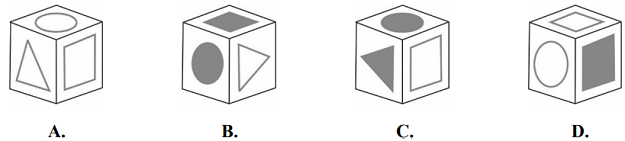
Który rysunek przedstawia kostkę sklejoną przez Mariusza? Wybierz właściwą odpowiedź spośród podanych.
 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Dany jest wzór opisujący pole trapezu: \(P=\frac{\left( x+y \right)\cdot h}{2},\) gdzie x i y oznaczają długości podstaw trapezu, a h oznacza wysokość trapezu.
Którym równaniem opisano x wyznaczone poprawnie z tego wzoru? Wybierz właściwą odpowiedź spośród podanych.
Kąt ostry rombu ma miarę 60°, a bok tego rombu ma długość równą 4 cm.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Krótsza przekątna dzieli ten romb na dwa trójkąty równoboczne. P/F
Pole tego rombu jest równe \(8\sqrt{3}\ c{{m}^{2}}.\) P/F
Na kartce w kratkę Tomek narysował według pewnej reguły cztery łamane (patrz rysunek).
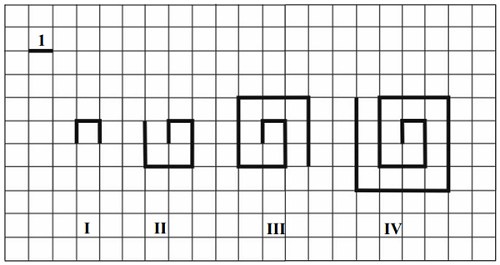
Długości tych łamanych zapisał w tabeli.

Kolejne łamane – od numeru V – Tomek rysował zgodnie z tą samą regułą.
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Łamana o długości 48 ma numer A/B
Łamana o numerze VIII ma długość C/D
W grudniu, w trzech sklepach sportowych: Alfa, Beta i Gamma, sprzedawano łyżwy figurowe w tej samej cenie. Na wiosnę w każdym sklepie ogłoszono obniżkę cen tych łyżew. Poniżej przedstawiono oferty tych sklepów.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Po obniżce cena łyżew figurowych była
Dany jest trójkąt równoboczny ABC o boku długości 10 cm. W tym trójkącie poprowadzono wysokość CD.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Obwód trójkąta ABC jest równy
W trójkącie KLM poprowadzono wysokość KN. Długości niektórych odcinków opisano za pomocą wyrażeń algebraicznych: \(\left| KL \right|=2y,\quad \left| LM \right|=2x,\quad \left| KN \right|=k+1.\)
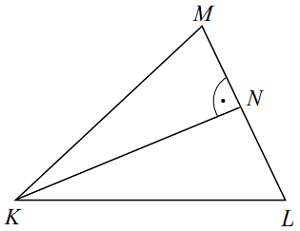
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole trójkąta KLM opisano wyrażeniem
Egzamin ósmoklasisty 2020 matematyka – zadania otwarte
W trójkącie o kątach wewnętrznych \(\alpha \,\beta \,\gamma \) miara kąta \(\alpha \) jest równa różnicy miar dwóch pozostałych kątów. Uzasadnij, że ten trójkąt jest prostokątny.
Treść dostępna po opłaceniu abonamentu.Na rysunku przedstawiono układ miejsc w przedziale ośmioosobowym wagonu kolejowego i zaznaczono kierunek jazdy pociągu.
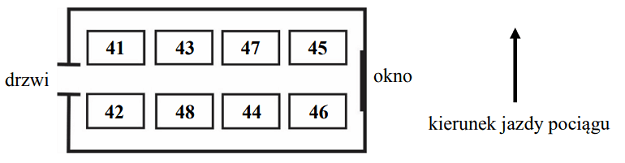
Edyta z Agnieszką planują zakup biletów na wspólną podróż. Wszystkie miejsca w przedziale są wolne. Edyta chce siedzieć przy oknie, natomiast Agnieszka chce siedzieć przodem do kierunku jazdy. Podaj wszystkie możliwości wyboru miejsc spełniające jednocześnie powyższe warunki. Zapisz rozwiązanie.
Treść dostępna po opłaceniu abonamentu.W domu kultury zorganizowano konkurs recytatorski. Dla uczestników kupiono nagrody: książki i e-booki. Książki stanowiły \(\frac{2}{3}\) liczby kupionych nagród. E-booków było o 8 mniej niż książek. Ile kupiono książek? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.W zakładzie krawieckim są szyte poduszki dla zwierząt domowych. Praca w tym zakładzie trwa pięć dni w tygodniu – od poniedziałku do piątku – po 7 godzin dziennie. W 2020 roku 1 marca wypadł w niedzielę i w tym miesiącu nie było żadnych dni wolnych oprócz sobót i niedziel. W ciągu każdej godziny pracy szyto średnio 3 poduszki. Ile poduszek uszyto w tym zakładzie w marcu 2020 roku? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Boisko szkolne ma kształt prostokąta o wymiarach 46 m i 30 m. Postanowiono posiać na nim trawę. Do obsiania 40m2 powierzchni jest potrzebny jeden kilogram nasion trawy. Nasiona trawy są sprzedawane tylko w 10-kilogramowych workach, po 163 zł za jeden worek. Oblicz koszt zakupu nasion trawy potrzebnych do obsiania tego boiska. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Podstawą ostrosłupa o wysokości H jest kwadrat. Na rysunku przedstawiono siatkę i podano długości niektórych krawędzi tego ostrosłupa.
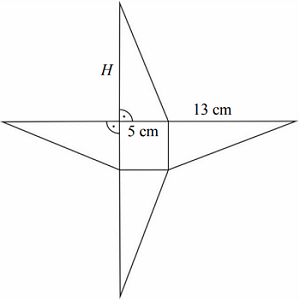
Oblicz objętość tego ostrosłupa. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.



