Testy ósmoklasisty – wybrane zadania z egzaminu gim. 2016
Zastęp harcerzy wyruszył z przystanku autobusowego do obozowiska. Na wykresie przedstawiono zależność między odległością harcerzy od obozowiska, a czasem wędrówki.
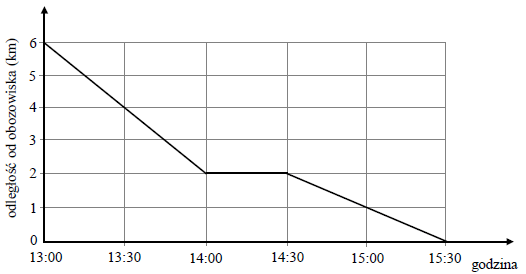
Które z poniższych zdań jest fałszywe? Wybierz właściwą odpowiedź spośród podanych.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Odległość między punktami, które na osi liczbowej odpowiadają liczbom \(-2,3\,\,i\,\,\frac{1}{3}\), jest równa
Z cyfr 2, 3 i 5 Ania utworzyła wszystkie możliwe liczby trzycyfrowe o różnych cyfrach. Które z poniższych zdań jest prawdziwe? Wybierz właściwą odpowiedź spośród podanych.
Rozwiązanie:
Dane są liczby:
Która z tych liczb jest największa? Wybierz właściwą odpowiedź spośród podanych.
Wskazówka: W tym zadaniu na egzaminie gimnazjalnym 2016 należało porównać zarówno podstawy i wykładniki. Jeśli nawet nie masz tych samych podstaw, czy wykładników to możesz obliczeniami sprowadzić liczby do takich samych liczby zarówno w podstawie jak i wykładniku. Przykład ma tak dobrane liczby, aby wybrane liczby łatwo było zamieniać na inne. Zerknij na film.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Liczba \(\sqrt[3]{81\cdot 64}\) jest równa
W tabeli podano, w jaki sposób zmienia się cena biletu na prom w ciągu całego roku.
| Cena podstawowa biletu na prom: 40 zł | ||
| Cena biletu | w sezonie zimowym | cena podstawowa obniżona o 20% |
| w sezonie letnim | cena podstawowa podwyższona o 200% | |
| poza sezonem zimowym i letnim | cena podstawowa | |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Bilet na prom w sezonie letnim jest droższy od biletu w sezonie zimowym o
Dane są liczby a i b takie, że 2 < a < 3 oraz –1 < b < 1.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli zdanie jest fałszywe.
W klasie IIIa liczba dziewcząt stanowi \(\frac{2}{3}\) liczby wszystkich uczniów tej klasy.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
W klasie IIIa
Cenę roweru obniżono o 8%. Klient kupił rower po obniżonej cenie i dzięki temu zapłacił o 120 zł mniej, niż zapłaciłby przed obniżką.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Przed obniżką ten rower kosztował
W pewnym zakładzie każdy z pracowników codziennie maluje taką samą liczbę jednakowych ozdób. Pracownicy potrzebowali 12 dni roboczych, aby wykonać zamówienie. Gdyby było ich o dwóch więcej, to czas wykonania tego zamówienia byłby o 3 dni krótszy.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczbę pracowników x tego zakładu można obliczyć, rozwiązując równanie
W układzie współrzędnych narysowano sześciokąt foremny o boku 2 tak, że jednym z jego wierzchołków jest punkt (0, 0), a jeden z jego boków leży na osi x (rysunek).
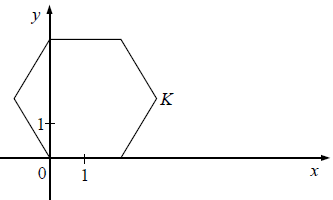
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Współrzędne wierzchołka K tego sześciokąta są równe
Do sześciokąta przedstawionego na rysunku w zadaniu 12. dorysowujemy kolejne takie same sześciokąty. Umieszczamy je tak, jak na rysunku, aby każdy następny sześciokąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego sześciokąta leżał na osi x. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, sześciokąty, które ponumerowano kolejnymi liczbami naturalnymi.
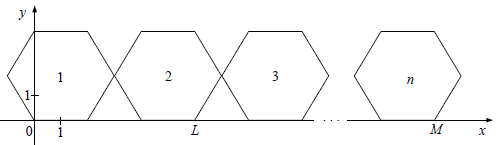
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli zdanie jest fałszywe.
Kasia ma 6 lat. Średnia arytmetyczna wieku Ani i Pawła jest równa 12 lat.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Średnia arytmetyczna wieku Kasi, Ani i Pawła jest równa
Na rysunku przedstawiono siatkę nietypowej sześciennej kostki do gry. Rzucamy jeden raz taką kostką.
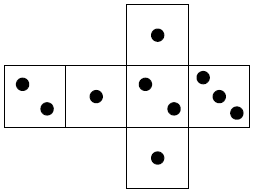
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli zdanie jest fałszywe.
Punkty E i F są środkami boków BC i CD kwadratu ABCD (rysunek).
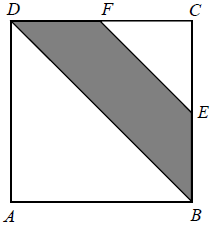
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli zdanie jest fałszywe.
Ewa narysowała kwadrat o boku 1, prostokąt o bokach 2 i 1 oraz kąt prosty o wierzchołku O.
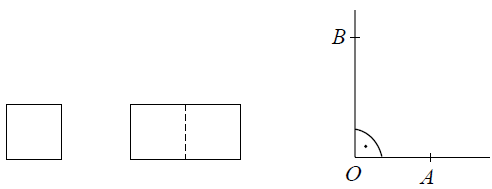
Następnie od wierzchołka O kąta prostego odmierzyła na jednym ramieniu kąta odcinek OA o długości równej przekątnej kwadratu, a na drugim ramieniu – odcinek OB o długości równej przekątnej prostokąta.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość odcinka AB jest równa
Wskazówka: Jest to bardzo ciekawe zadanie wykorzystujące twierdzenie Pitagorasa
Każdy bok kwadratu ABCD podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano ośmiokąt (rysunek).
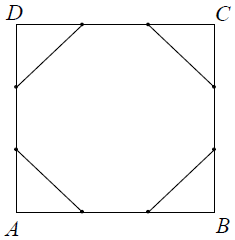
Które z poniższych zdań jest prawdziwe? Wybierz właściwą odpowiedź spośród podanych.
Na rysunku poniżej przedstawiono siatkę sześcianu. Punkty: P, S, T, W, Z są środkami jego krawędzi.
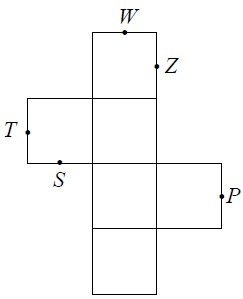
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Po złożeniu sześcianu z tej siatki punkt P pokryje się z punktem
Jedenaście piłeczek, ponumerowanych kolejnymi liczbami naturalnymi od 1 do 11, wrzucono do pudełka. Janek, nie patrząc na piłeczki, wyjmuje je z pudełka. Ile najmniej piłeczek musi wyjąć Janek, aby mieć pewność, że przynajmniej jedna wyjęta piłeczka jest oznaczona liczbą parzystą? Odpowiedź uzasadnij.
Uczniowie klas trzecich pewnego gimnazjum pojechali na wycieczkę pociągiem. W każdym zajętym przez nich przedziale było ośmioro uczniów. Jeśli w każdym przedziale byłoby sześcioro uczniów, to zajęliby oni o 3 przedziały więcej. Ilu uczniów pojechało na tę wycieczkę? Zapisz obliczenia.




