Testy ósmoklasisty – Zbiór zadań egzaminacyjnych CKE: zadania od 19 do 36
Egzamin ósmoklasisty matematyka, testy 8 klasisty, arkusze próbne, odpowiedzi ⇒Zobacz więcej⇐Na diagramie przedstawiono wielkość produkcji krzeseł w firmie Mebelix w 2015 r. i 2016 r.
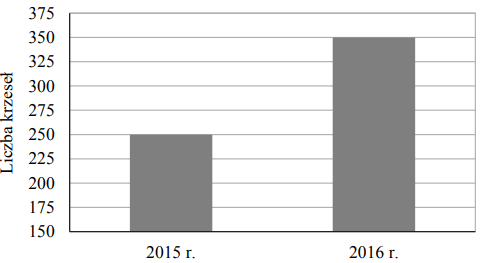
Czy liczba wyprodukowanych krzeseł w roku 2016 była o 100% większa od liczby wyprodukowanych krzeseł w roku 2015? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.

Na rysunku przedstawiono kwadraty ABCD, EAOD i BFCO. Punkt O jest punktem przecięcia przekątnych kwadratu ABCD.
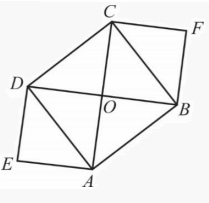
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Drewnianą kostkę sześcienną o krawędzi długości 30 cm rozcięto na 27 jednakowych mniejszych sześciennych kostek. Z ośmiu takich małych kostek ułożono nowy sześcian.
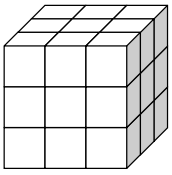
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
W tabeli podano wybrane informacje na temat dwóch rodzajów herbat, które pije rodzina Nowaków.

Rodzina ta wypija dziennie średnio 12 kubków herbaty i zamierza kupić możliwie najmniejszą liczbę opakowań herbaty jednego rodzaju, aby wystarczyło jej na 30 dni. Oblicz koszt zakupu herbaty sypkiej oraz koszt zakupu herbaty w torebkach. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Uzasadnij, że pierwszy dzień września i pierwszy dzień grudnia tego samego roku wypadają w tym samym dniu tygodnia.
Treść dostępna po opłaceniu abonamentu.W układzie współrzędnych na płaszczyźnie dane są punkty: K=(–2,8) i M=(4,6). Podaj współrzędne punktu P takiego, że jeden z trzech punktów P, K, M jest środkiem odcinka o końcach w dwóch pozostałych punktach. Podaj wszystkie możliwości.
Treść dostępna po opłaceniu abonamentu.W tabeli przedstawiono ceny kupna i sprzedaży dwóch walut w kantorze Pik.

Marcin chce wymienić 400 funtów brytyjskich na dolary. W tym celu musi najpierw wymienić funty na złotówki, a następnie – otrzymane złotówki na dolary. Ile dolarów otrzyma Marcin, jeżeli wymieni walutę w kantorze Pik? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Bok CD kwadratu ABCD podzielono punktami E i F na trzy odcinki równej długości. Przez wierzchołek A kwadratu i przez punkt E poprowadzono prostą. Pole trójkąta AED wynosi 24cm2. Oblicz pole kwadratu ABCD. Zapisz obliczenia..
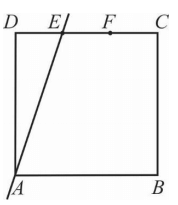 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
W pierwszym zbiorniku było czterokrotnie więcej wody niż w drugim. Po wlaniu 6 litrów wody do każdego z nich, w pierwszym jest dwukrotnie więcej wody niż w drugim. Ile łącznie wody jest teraz w obu zbiornikach? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Prostokąt ABCD podzielono na 6 kwadratów: jeden duży, dwa średnie i trzy małe, jak na rysunku.
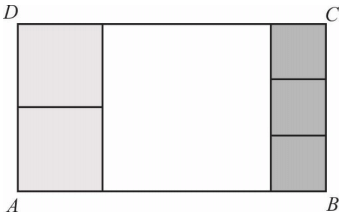
Uzasadnij, że pole powierzchni dużego kwadratu jest większe niż połowa powierzchni prostokąta ABCD.
Treść dostępna po opłaceniu abonamentu.Prostokątny pasek papieru pocięto na cztery części w sposób przedstawiony na rysunku 1. Z tych części ułożono figurę w kształcie kwadratu tak, jak pokazano na rysunku 2. Pole tego kwadratu jest równe 36cm2.
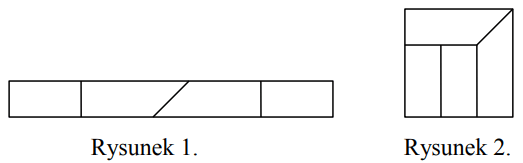
Oblicz obwód paska papieru przed pocięciem. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Trzy sąsiadki zamówiły wspólnie kawę w sklepie internetowym. Kawa dla pani Malinowskiej miała kosztować 120 zł, a dla pani Wiśniewskiej i pani Śliwińskiej – po 90 zł. Jednak przy zakupie otrzymały rabat i za zamówioną kawę zapłaciły tylko 260 zł. Ile pieniędzy powinna zapłacić każda z pań, aby jej wpłata była proporcjonalna do pierwotnej wartości zamówienia? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Proste a i b są równoległe.
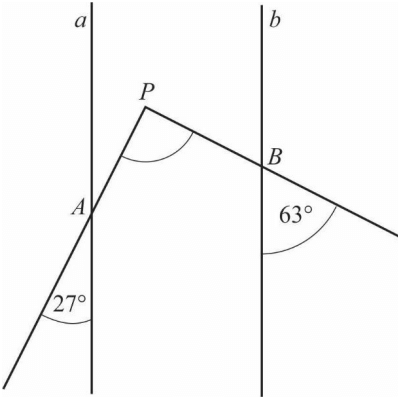
Półproste PA i PB przecinają te proste, w wyniku czego tworzą z nimi kąty ostre o miarach podanych na rysunku. Uzasadnij, że kąt APB jest prosty.
Treść dostępna po opłaceniu abonamentu. 2 SPOSÓB Treść dostępna po opłaceniu abonamentu.W pojemniku znajdują się niebieskie, czarne i zielone piłeczki. Czarnych piłeczek jest o 20% mniej niż niebieskich, a niebieskich – o 6 mniej niż zielonych. Niebieskich i zielonych piłeczek jest łącznie o 48 więcej niż czarnych. Ile jest wszystkich piłeczek w tym pojemniku? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Trójkąt przedstawiony na rysunku jest ścianą boczną ostrosłupa prawidłowego trójkątnego.
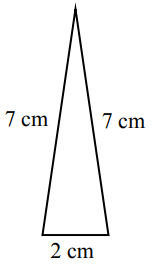
Oblicz pole powierzchni całkowitej tego ostrosłupa. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Jaskinię Książęcą może zwiedzić codziennie tylko dziesięć grup, które wchodzą po jednej w jednakowych odstępach czasu. Pierwsza grupa rozpoczyna zwiedzanie o 9:00, a ostatnia – o 16:30. Grupa harcerzy przyszła zwiedzić jaskinię o godzinie 13:25. Ile co najmniej minut harcerze będą czekali na wejście do jaskini? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Agnieszka zapisała liczbę czterocyfrową podzielną przez 7. Skreśliła w tej liczbie cyfrę jedności i otrzymała liczbę 496. Jaką liczbę czterocyfrową zapisała Agnieszka? Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.Prostokąt o bokach długości 12 i 6 podzielono na dwa prostokąty (patrz rysunek).
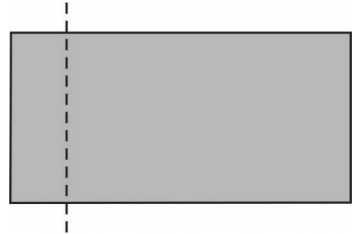
Obwód jednego z prostokątów otrzymanych w wyniku podziału jest 2 razy większy od obwodu drugiego. Podaj wymiary prostokąta o mniejszym obwodzie. Zapisz obliczenia.
Treść dostępna po opłaceniu abonamentu.



