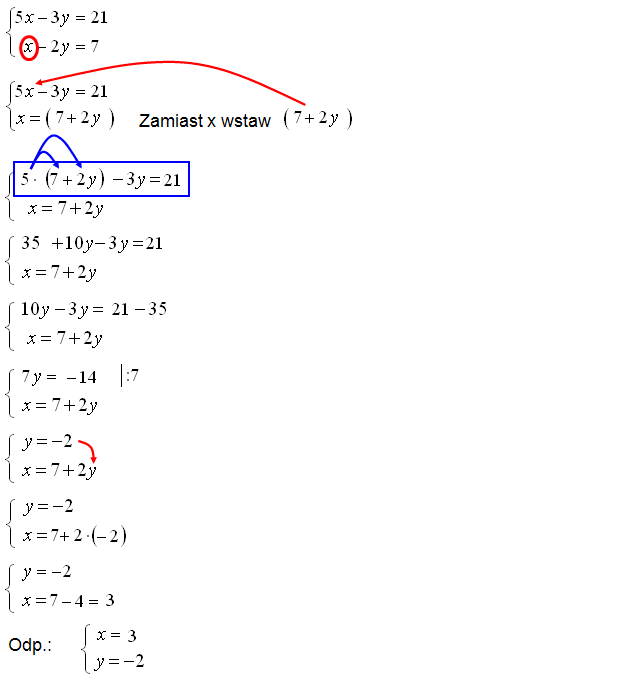Rozwiąż układ równań metodą podstawiania
Układy równań najczęściej rozwiązuje się metodą podstawiania, która zostanie omówiona na podstawie konkretnego przykładu.
Teraz rozwiążemy krok po kroku układ równań metodą podstawiania.
Metoda podstawiania przez wyznaczenie zmiennej x.
Krok 1: W naszym układzie równań w II równaniu zauważamy „samotną literkę x”. „Samotna literka” to żargon jakim określam literkę x lub y, przy której stoi współczynnik „1”. Oczywiście w rzeczywistości pisząc np.: „x” wiemy, że to „1x”, ale cyfra „1” jest pomijana w zapisie. Mówiąc ogólnie metoda podstawiania w prostych przykładach polega na znalezieniu x-sa lub y-ka bez liczby i wyznaczeniu z danego równania niewiadomej x lub y.

Uwaga: Jeśli przy wszystkich niewiadomych stoją liczby (różne od 1) wówczas możesz jedno z równań podzielić przez jeden ze współczynników w celu uzyskania „samotnej niewiadomej”.
Krok 2: W poniższym układzie równań wyznaczasz „samotną zmienną x” z II równania, czyli x-sa zostawiasz z lewej strony, a „-2y” przenosisz na prawą stronę. Zajmujesz się tylko II równaniem z „samotną literką”. W wybranym równaniu „samotną literkę” zostawiasz z lewej strony, a pozostałe elementy przenosisz na stronę prawą. Prawa strona tego równania jest Twoim podstawieniem (7+2y).
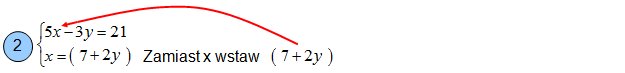
Krok 3: W miejsce x-sa w I równaniu podstawiasz wyrażenie (7+2y) – Twoje podstawienie. Jeśli nie rozumiesz możesz przepisać całe I równanie ołówkiem: 5x-3y=21. Teraz zetrzyj symbol x w I równaniu, a w jego miejsce wstaw otrzymane podstawienie: (7+2y). Drugie równanie przepisujesz bez zmiany.

Krok 4: Rozwiązujesz chwilowo tylko I równanie. W naszym układzie wymnażasz liczbę 5 przez nawias (7+2y).

Krok 5: Rozwiązując I równanie grupujesz wyrażenia z niewiadomą y po lewej stronie, a liczby umieszczasz z prawej strony.

Krok 6: W I równaniu redukujesz z lewej strony niewiadome y, zaś z prawej strony redukujesz liczby. Jeśli przy niewiadomej y jest liczba różna od „1” wówczas podziel równanie przez liczbę stojącą przy niewiadomej. Tu równanie dzielimy przez 7.

Krok 7: W pierwszym równaniu otrzymujesz obliczonego y-ka. tzn. otrzymujesz y=-2. W tym momencie zauważasz, że y-ka o wartości liczbowej „-2” możesz wstawić do II równania.

Krok 8: Wstawiasz do II równania w miejsce niewiadomej y jej wartość. Jeśli nadal nie rozumiesz po prostu przepisz ołówkiem II równanie (Twoje podstawienie). Teraz zetrzyj tylko niewiadomą y. W jej miejsce wpisz obliczoną liczbę z I równania „-2”.

Krok 9: Pierwsze równanie y=-2 przepisujesz bez zmiany, zaś II równanie obliczasz. Wykonujesz mnożenie, a następnie dodajesz liczby.

Krok 10: Na końcu należy jeszcze podsumować układ równań rozwiązywany metodą podstawiania przez połączenie liczb klamerkami.

Zobacz, przeanalizuj i rozwiąż układ równań metodą podstawiania. Jest to metoda skuteczniejsza od metody przeciwnych współczynników, ponieważ istnieją trudniejsze przypadki, które można rozwiązać tylko przy pomocy metody podstawiania. Istnieje tutaj pewien schemat postępowania, według którego należy rozwiązywać zadania.
Jak rozwiązać układ równań metodą podstawiania w zadaniach?
Rozwiąż układ równań metodą podstawiania.
\[\left\{ {\begin{array}{*{20}{c}} {3x – 2y = – 2}\\ {2x + y = – 6} \end{array}} \right.\]Rozwiąż układ równań metodą podstawiania.
\[\left\{ {\begin{array}{*{20}{c}} {\frac{4}{5}x + \frac{2}{5}y = 2}\\ {\frac{3}{2}x + \frac{5}{2}y = \frac{{25}}{2}} \end{array}} \right.\]W tym układzie równań na samym początku warto usunąć mianowniki. Robisz to przez pomnożenie równania przez liczbę, która jest wspólnym mianownikiem, mianowników występujących w danym równaniu.
Rozwiąż układ równań (Metoda podstawiania).
\[\left\{ {\begin{array}{*{20}{c}} {\frac{2}{3}x + \frac{3}{4}y = 8}\\ {\frac{1}{2}x – \frac{1}{5}y = – \frac{1}{{10}}} \end{array}} \right.\]Rozwiąż układ równań.
\[\left\{ {\begin{array}{*{20}{c}} {\frac{3}{4}x – \frac{4}{5}y = x – y\quad \quad \quad }\\ {3\left( {4 – x} \right) – 5\left( {y – 1} \right) = – 20} \end{array}} \right.\]Zobacz, jak rozwiązać układ równań metodą przeciwnych współczynników?