Twierdzenie Pitagorasa – sprawdzian – zadania
–- Twierdzenie Pitagorasa – sformułowanie
- Twierdzenie Pitagorasa – dowód
- Trójkąt pitagorejski i egipski
- Zastosowanie twierdzenia Pitagorasa
- Twierdzenie Pitagorasa w układzie współrzędnych
- Twierdzenie odwrotne do Twierdzenia Pitagorasa
- Wzór na przekątną kwadratu
- Twierdzenie Pitagorasa – sprawdzian – zadania
Zadania na Twierdzenie Pitagorasa warto rozpocząć od przykładów, w których ćwiczy się równość między polami kwadratów zbudowanych na przyprostokątnych, a polem kwadratu zbudowanego na przeciwprostokątnej.
Oblicz pole kwadratu zbudowanego na boku trójkąta prostokątnego.
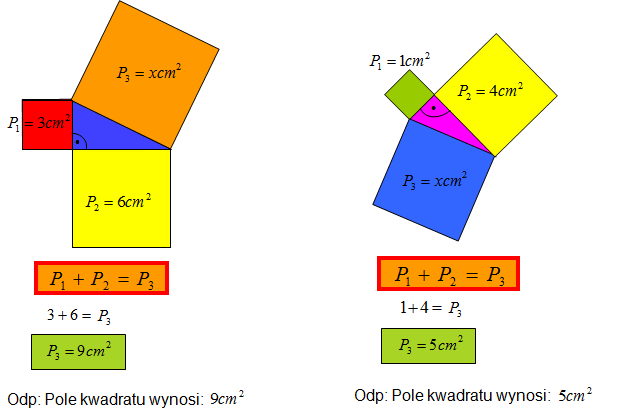
Oblicz pole kwadratu zbudowanego na boku trójkąta prostokątnego.

Oblicz pole kwadratu zbudowanego na boku trójkąta równoramiennego prostokątnego.

Oblicz przeciwprostokątną w trójkącie prostokątnym o danych przyprostokątnych: 3 i 4.
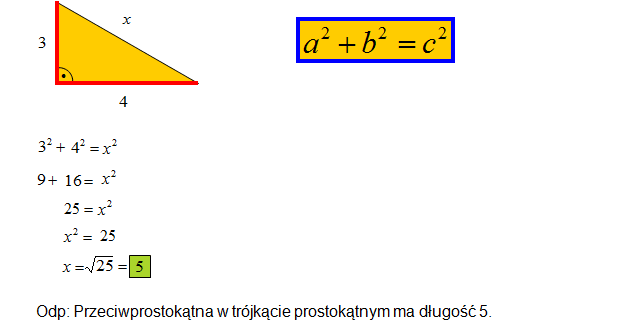
W tym zadaniu dowiedziałeś się jak obliczyć przeciwprostokątną? Jak zauważyłeś należy, krótsze boki(przyprostokątne) dodać do siebie z kwadratami, a otrzymana suma kwadratów przyprostokątnych jest równa długości przeciwprostokątnej do kwadratu.
Oblicz brakujący bok w trójkącie prostokątnym.

Zadanie pokazuje jak obliczyć przyprostokątną? W trójkącie prostokątnym masz oznaczone boki niewiadomą „x” oraz danymi liczbami. Wstawiasz więc oznaczenia boków do wzoru na Twierdzenie Pitagorasa podawanego najczęściej w postaci: a2 + b2 = c2. Dodajesz z kwadratami krótsze boki, czyli przyprostokątne. Otrzymana suma jest równa przeciwprostokątnej podniesionej do kwadratu. Dalej rozwiązujesz otrzymane równanie. Już na pewno wiesz jak obliczyć przyprostokątną!
Oblicz brakujące boki wykorzystując Twierdzenie Pitagorasa.
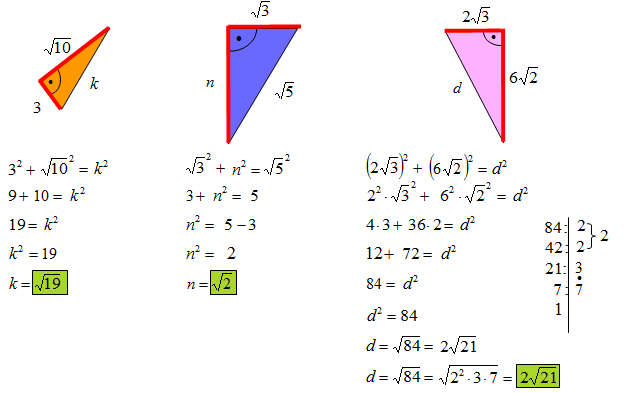
Wykorzystując Twierdzenie Pitagorasa, oblicz brakujący bok trójkąta.

Zadanie przedstawione wyżej pokazuje jak obliczyć przyprostokątną (pierwszy trójkąt) oraz jak obliczyć przeciwprostokątną(drugi trójkąt). Największą tutaj trudnością jest podnoszenie do potęgi pierwiastka opisującego długość boku trójkąta. W tego typu zadaniach kwadrat likwiduje się z pierwiastkiem.
Oblicz obwód niebieskiego trójkąta.

Powyższe zadanie jest o podwyższonym stopniu trudności, ponieważ należy zastosować Twierdzenie Pitagorasa dwa razy. Raz, aby obliczyć literkę „x”, a następnie, aby obliczyć literkę „y”.
Twierdzenie Pitagorasa – zadania z treścią
Zadania z treścią związane z Twierdzeniem Pitagorasa chciałbym zacząć od dość trudnego zadania jakim jest konstrukcja pierwiastka z danej liczby. Jest ona oparta właśnie na Twierdzeniu Pitagorasa.
Niżej przedstawiam kilka zadań, w których trzeba wykazać się umiejętnością konstrukcji i Twierdzenia Pitagorasa.
- Konstrukcja pierwiastka z liczby 5
- Wyznacz konstrukcyjnie odcinek o długości pierwiastka z liczby 20.
- Wyznacz konstrukcyjnie odcinek o długości pierwiastek z 7.
- Wyznacz konstrukcyjnie odcinek o długości pierwiastek z liczby 28.
Budowa domów drewnianych wykonanych w technologii szkieletowej polega na wykonaniu drewnianego szkieletu, który służy jako rusztowanie do dalszej budowy, co ilustruje rysunek. W celu wzmocnienia budowli przed niszczącym działaniem wiatru stosuje się tzw. zastrzały, czyli ukośne belki, które zabezpieczają budowlę przed wykrzywieniem. Oblicz długość skośnej belki zaznaczonej na czarno.
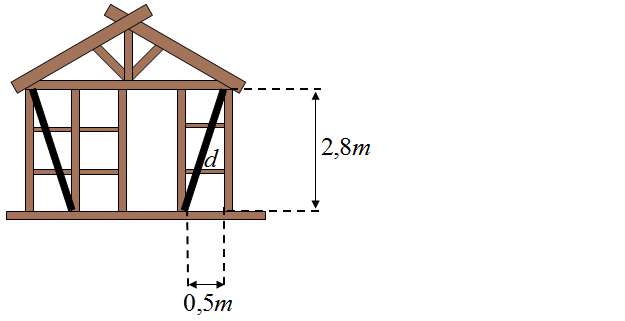
Przedstawione zadanie jest matematyczne, ale również pokazuje jak w praktyce zastosować Twierdzenie Pitagorasa?
Oblicz obwód kwadratu o przekątnej 6 wykorzystując Twierdzenie Pitagorasa.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
W trapezie równoramiennym przekątna o długości 13cm tworzy z ramieniem kąt prosty. Oblicz pole tego trapezu, jeśli górna podstawa wynosi 1dm, i jest dwa razy dłuższa od wysokości.
Treść dostępna po opłaceniu abonamentu.Rysunek przedstawia fragment mapy pewnego miasta. Pomarańczowym kolorem zaznaczono trasę przejazdu karetki pogotowia. Obok zaznaczono ilość pokonanych metrów. Oblicz, o ile krótszą drogę pokonałaby karetka, gdyby pokonałaby trasę w linii prostej od punktu startu do docelowego miejsca.
Treść dostępna po opłaceniu abonamentu.W trójkącie równoramiennym wysokość o długości 4cm jest opuszczona na podstawę o długości 10cm. Oblicz obwód tego trójkąta.
Treść dostępna po opłaceniu abonamentu.Oblicz na jakiej wysokości znajdzie się taczka (H=?), jeśli w chwili obecnej znajduje się na wysokości 2m. Długość czerwonej kładki wynosi 4m, rów z wodą ma szerokość 3m.
Treść dostępna po opłaceniu abonamentu.Romb zbudowany jest z 2 trójkątów równoramiennych o bokach 6, 6, 8. Podaj długości przekątnych tego rombu.
Treść dostępna po opłaceniu abonamentu.Z kulistego arbuza o średnicy 26cm odcięto jego część o grubości 8cm, tak jak pokazuje rysunek. Oblicz powierzchnię (czerwonego) pola przekroju arbuza.
Treść dostępna po opłaceniu abonamentu.Kłodę drewna o średnicy 20cm pocięto na deski o grubości 5cm każda. Oblicz szerokość pierwszej deski po odcięciu.
Treść dostępna po opłaceniu abonamentu.Z punktu A leżącego na okręgu wychodzą dwie cięciwy o długości 5 i 10, które tworzą kąt prosty. Oblicz promień danego okręgu.
Treść dostępna po opłaceniu abonamentu.Dany jest trójkąt równoramiennym ABC o bokach 13, 13, 10. Punkt D leży na podstawie AB tego trójkąta w taki sposób, że |AD|=3. Oblicz długość odcinka |CD| (Patrz na rysunek).
Treść dostępna po opłaceniu abonamentu.Oblicz obwód, pole oraz przekątne w trapezie AECD. Patrz na rysunek.
Treść dostępna po opłaceniu abonamentu.W okrąg o średnicy 10cm wpisano trapez równoramienny o ramionach 4cm w taki sposób, że dolna podstawa trapezu leży na średnicy okręgu. Oblicz przekątną i wysokość trapezu.
Treść dostępna po opłaceniu abonamentu.



