Definicja pierwiastka – jak się liczy pierwiastki?
- Definicja pierwiastka
- Pierwiastki – wzory
- Pierwiastek z pierwiastka
- Szacowanie pierwiastków
- Wyłączanie czynnika przed znak pierwiastka
- Włączanie czynnika pod znak pierwiastka
- Mnożenie i dzielenie pierwiastków tego samego stopnia
- Dodawanie i odejmowanie pierwiastków
- Pierwiastek z potęgi
- Usuwanie niewymierności z mianownika
- Potęga o wykładniku wymiernym, a pierwiastkowanie
- 8 klasa – Spis treści powtórek przed egzaminem w tym także pierwiastki

Definicja pierwiastka:
Poniższy zapis czytamy:
\[\sqrt[n]{a} = b\quad ,gdy\quad {b^n} = a\]„Pierwiastek n-tego stopnia z liczby a równa się b, gdy b do potęgi n-tej jest równe a”
W tej definicji:
n – stopień pierwiastka
a – liczba podpierwiastkowa
b – pierwiastek n-tego stopnia z liczby a, wynik pierwiastkowania
Jak obliczać pierwiastki? Na początku zastanawiasz się, jaki jest stopień pierwiastka? W zapisie \(\sqrt[3]{8}\) jest on jawnie podany. To ta mała trójeczka decyduje, że jest to pierwiastek trzeciego stopnia inaczej pierwiastek sześcienny.
Gdy nie ma jawnie zapisanego stopnia pierwiastka to wiemy, że jest to pierwiastek 2-go stopnia, czyli pierwiastek kwadratowy. Zerknij na równoważność zapisów: \(\sqrt[2]{9}= \sqrt{9}\).
Na początku zauważ, że pierwiastkowanie jest działaniem odwrotnym do potęgowania.
\[\sqrt[3]{8}=2\quad ,bo\quad {{2}^{3}}=8\]Jeśli chcesz obliczyć pierwiastek, np. \(\sqrt[3]{8}=\) zastanawiasz się jaka liczba podniesiona do potęgi 3 da Ci liczbę 8. Zauważasz, że \({{2}^{3}}=8\). Dlatego zapoznanie się definicją pierwiastka jest ściśle związana z umiejętnością potęgowania. Mam nadzieję, że już wiesz jak się liczy pierwiastki i rozumiesz definicję pierwiastka.
Tabliczka pierwiastkowania wykorzystuje definicję pierwiastków
Zaczynając przygodę z pierwiastkami powtórz tabliczkę mnożenia oraz tzw. tabliczkę pierwiastkowania. Wówczas obliczanie pierwiastków nie będzie Ci straszne.
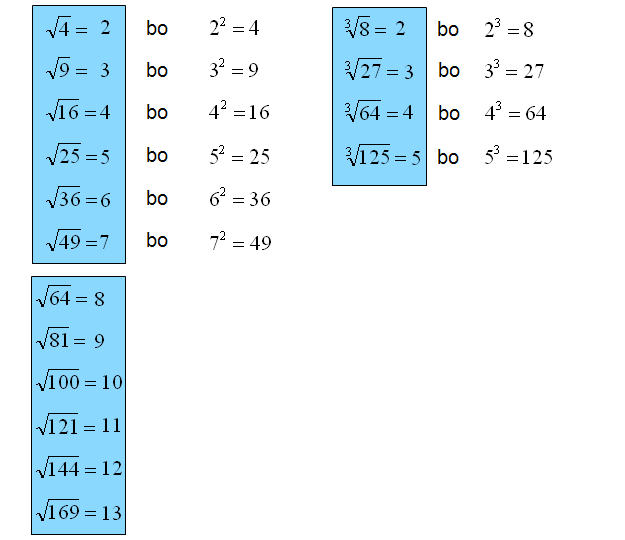
Pierwiastki – zadania łatwe
Oblicz pierwiastek kwadratowy.
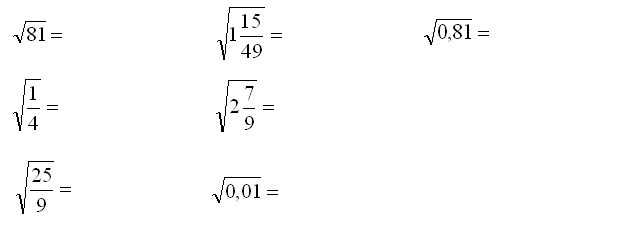
Przeanalizujmy pierwszy przykład: \(\sqrt{81}\). Jest to pierwiastek kwadratowy, czyli drugiego stopnia. Jeśli nie ma zaznaczonego stopnia pierwiastka to domyślnie jest to pierwiastek kwadratowy (drugiego stopnia) np. \(\sqrt{81}=\sqrt[2]{81}\).
Jak widzisz pierwiastkowanie w zadaniach jest bardzo proste!
Chcąc obliczyć \(\sqrt{81}\) zastanawiasz się jaka liczba podniesiona do potęgi 2 daje liczbę 81. Wiemy, że \({{9}^{2}}=81\), zatem pierwiastek jest równy 9.
Podsumujmy: \(\sqrt{81}=9\quad ,bo\quad {{9}^{2}}=81\)
Zerknijmy jeszcze na przykład \(\sqrt {1\frac{{15}}{{49}}}\). Na pierwszy rzut oka nie można obliczyć pierwiastka. Po chwili zastanowienia można zamienić ułamek mieszany na niewłaściwy, czyli pozbyć się całości, a następnie obliczyć pierwiastek z ułamka niewłaściwego: \[\sqrt {1\frac{{15}}{{49}}} = \sqrt {\frac{{64}}{{49}}} = \frac{8}{7}\]
Oblicz pierwiastek sześcienny.
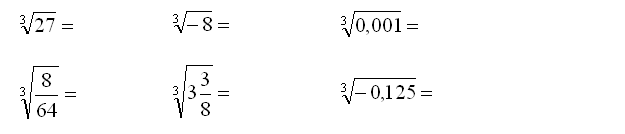
Zerknijmy jak obliczać pierwiastki sześcienne (trzeciego stopnia). Jak obliczyć pierwiastek sześcienny z liczby 27: \(\sqrt[3]{27}\)?
Zadajesz sobie strategiczne pytanie: „Jaka liczba podniesiona do potęgi 3 daje liczbę 27?”. Odpowiedź nie jest trudna: „Jest to liczba 3”. Zatem podsumujmy:
\(\sqrt[3]{27}=3\), ponieważ \({{3}^{3}}=27\)
Omówmy jeszcze \(\sqrt[3]{3\frac{3}{8}}\). Zauważasz po krótkim namyśle, że najpierw trzeba zamienić liczbę podpierwiastkową na ułamek niewłaściwy. Mamy wówczas \(\sqrt[3]{\frac{27}{8}}\). W kolejnym kroku zastanawiasz się jaka liczba podniesiona do potęgi 3 daje Ci ułamek \(\frac{27}{8}\). Jest to liczba \(\frac{3}{2}\).
Podsumujmy: \[\sqrt[3]{{3\frac{3}{8}}} = \sqrt[3]{{\frac{{27}}{8}}} = \frac{3}{2}\quad ,bo\quad {\left( {\frac{3}{2}} \right)^3} = \frac{{27}}{8}\]
- Definicja pierwiastka
- Pierwiastki – wzory
- Pierwiastek z pierwiastka
- Szacowanie pierwiastków
- Wyłączanie czynnika przed znak pierwiastka
- Włączanie czynnika pod znak pierwiastka
- Mnożenie i dzielenie pierwiastków tego samego stopnia
- Dodawanie i odejmowanie pierwiastków
- Pierwiastek z potęgi
- Usuwanie niewymierności z mianownika
- Potęga o wykładniku wymiernym, a pierwiastkowanie
- 8 klasa – Spis treści powtórek przed egzaminem w tym także pierwiastki