Konkurs kuratoryjny z matematyki 2013/14 – Śląskie – Etap rejonowy
Rozwiąż krzyżówkę, wpisując w odpowiednie miejsca liczby opisane w pytaniach. Zaznaczone pola rozwiązanej krzyżówki zawierają kolejne cyfry rozwinięcia dziesiętnego liczby Eulera (zwaną również liczbą Nepera), którą oznaczamy krótko literą e.
a. Sześcian najmniejszej liczby pierwszej nieparzystej.
b. Rozwiązanie równania \(\frac{{\sqrt 2 }}{x} = \frac{{\sqrt 6 }}{{\sqrt 3 }}\)
c. Rozwiązanie równania \(3 + 40:x \cdot 2 = 13\)
d. Liczba, której 35% wynosi 700.
e. Liczba, która nie należy do dziedziny funkcji \(f\left( x \right) = \frac{1}{{512 – {x^3}}}\)
f. Mianownik liczby odwrotnej do 1,11.
g. Liczba zer w zapisie dziesiętnym liczby sto milionów.
h. Liczb niepodzielna przez 36 spośród liczb: \[162436, 162432, 366336.\]
i. Sześcian parzystej liczby pierwszej.
j. Mediana zbioru liczb: \[16, 4, 11, 18, 9, 8, 13, 19, 16, 10, 16, 9, 20, 14, 15.\]
k. Miejsce zerowe funkcji \(y = \frac{1}{5}x – 3.\)
l. Wartość bezwzględna najmniejszej ujemnej liczby czterocyfrowej
m. Najmniejsza trzycyfrowa liczba pierwsza
n. Pole powierzchni kuli, która powstała przez obrót koła o polu \(100\,{j^2}\) wokół średnicy.
o. Objętość graniastosłupa o takiej samej podstawie i wysokości, jaką ma ostrosłup o objętości \(117\,{j^3}\)
p. Wartość współczynnika b funkcji liniowej y = 4x – b , dla której liczba 31 jest miejscem zerowym.
q. Wartość \(\frac{{\sqrt[3]{{108}}}}{{\sqrt[3]{4}}}\)
Liczby a i b są naturalne. Reszty z dzielenia tych liczb przez 5 są równe odpowiednio 4 i 3.
- Reszta z dzielenia sumy tych liczb przez 5 jest równa 3. PRAWDA/FAŁSZ
- Reszta z dzielenia iloczynu tych liczb przez 5 jest równa 2. PRAWDA/FAŁSZ
- Jeżeli a > b , to reszta z dzielenia różnicy a – b przez 5 jest równa 1. PRAWDA/FAŁSZ
Jeżeli \(a=\frac{17}{66},b=\frac{1717}{6666},c=\frac{17171717}{66666666}\) to prawdziwe jest wyrażenie
- a ≤ b PRAWDA/FAŁSZ
- a = b = c PRAWDA/FAŁSZ
- b ≥ c PRAWDA/FAŁSZ
Jeżeli \(\frac{2a}{a+b}=\frac{4}{5},\) to \(\frac{2b}{b+a}\) jest
- liczbą całkowitą. PRAWDA/FAŁSZ
- równe \(\frac{6}{5}.\) PRAWDA/FAŁSZ
- liczbą wymierną. PRAWDA/FAŁSZ
Rysunek przedstawia wykres funkcji f(x).
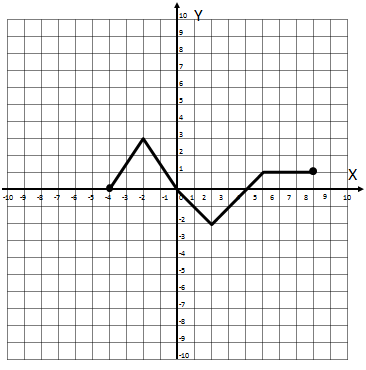
- Dziedziną funkcji f(x) są wszystkie liczby mniejsze od 8 i większe od –4. PRAWDA/FAŁSZ
- Funkcja f(x) ma dwa miejsca zerowe . PRAWDA/FAŁSZ
- Funkcja f(x) przyjmuje wartość równą 1 tylko dla argumentu 8. PRAWDA/FAŁSZ
Każdą liczbę można przedstawić w postaci
- ilorazu dwóch liczb o różnych znakach. PRAWDA/FAŁSZ
- sumy dwóch liczb o różnych znakach. PRAWDA/FAŁSZ
- różnicy dwóch liczb o różnych znakach. PRAWDA/FAŁSZ
Liczbą naturalną jest
- \(\frac{{{10}^{85}}+2}{6}\) PRAWDA/FAŁSZ
- \(\frac{{{5}^{127}}+1}{2}\) PRAWDA/FAŁSZ
- \(\frac{{{10}^{999}}-1}{9}\) PRAWDA/FAŁSZ
Dany jest sześcian o krawędzi a.
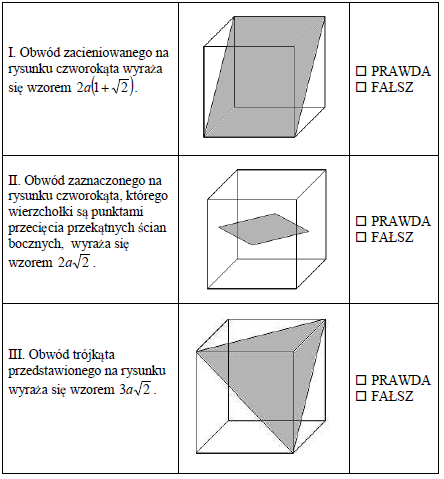
- Obwód zacieniowanego na rysunku czworokąta wyraża się wzorem \(2a\left( 1+\sqrt{2} \right)\) PRAWDA/FAŁSZ
- Obwód zaznaczonego na rysunku czworokąta, którego wierzchołki są punktami przecięcia przekątnych ścian bocznych, wyraża się wzorem \(2a\sqrt{2}\) PRAWDA/FAŁSZ
- Obwód trójkąta przedstawionego na rysunku wyraża się wzorem \(3a\sqrt{2}\) PRAWDA/FAŁSZ
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
W trapezie równoramiennym o polu 60 cm² ramię ma długość 10 cm, a wysokość 6 cm.
- Podstawy trapezu mają długość 20 cm i 4 cm. PRAWDA/FAŁSZ
- Obwód trapezu wynosi 40 cm. PRAWDA/FAŁSZ
- Kąt ostry trapezu ma miarę 60°. PRAWDA/FAŁSZ
Uzasadnij, że dwusieczne dwóch sąsiednich kątów wewnętrznych równoległoboku są prostopadłe.
Treść dostępna po opłaceniu abonamentu.Wczoraj w klasie uczniów obecnych było 8 razy tyle co nieobecnych. Dzisiaj wrócił do szkoły jeden uczeń i teraz nieobecni stanowią 8% uczniów obecnych. Oblicz, ilu uczniów liczy klasa?
Treść dostępna po opłaceniu abonamentu.Prawdopodobieństwo trafienia w określoną część tarczy strzeleckiej określamy, jako stosunek pola tej części do pola całej tarczy. Rysunek przedstawia tarczę podzieloną na 5 części, przy czym promień najmniejszego okręgu wynosi r, a promień każdego kolejnego okręgu jest o r większy od poprzedniego. Jakie jest prawdopodobieństwo trafienia w zacienioną jej część? Zakładamy, że żaden strzał nie jest chybiony.
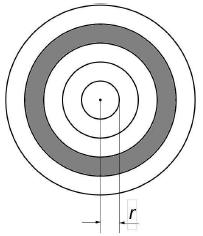 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Dwa okręgi o promieniach 2 cm i 6 cm są styczne zewnętrznie. Oblicz pole powierzchni figury ograniczonej tymi okręgami i prostą styczną do obu okręgów.
Treść dostępna po opłaceniu abonamentu.Iloczyn sumy dwóch liczb całkowitych przez ich różnicę jest równy 20. Podaj wszystkie pary liczb spełniających ten warunek. Odpowiedź uzasadnij.
Treść dostępna po opłaceniu abonamentu.



