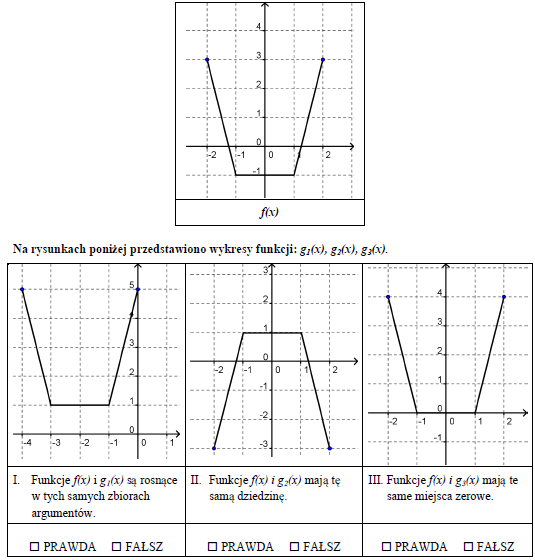
Konkurs kuratoryjny z matematyki 2012/13 – Śląskie – Etap wojewódzki
Niżej znajdują się zadania matematycznego konkursu kuratoryjnego etapu wojewódzkiego z województwa śląskiego z roku 2012-2013 wraz z rozwiązaniami.
Rozwiąż krzyżówkę. Hasło – nazwę wielościanu przedstawionego na rysunku u dołu strony – odczytasz w zacieniowanych okienkach. Nie jest ono oceniane, ale zweryfikuje Twoje odpowiedzi.
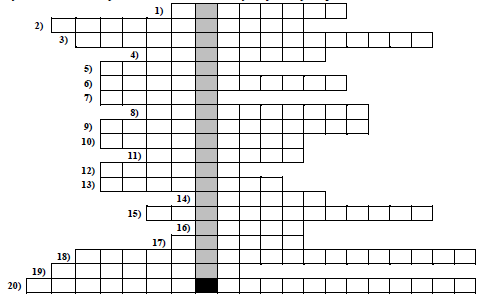
1. Najdłuższa cięciwa.
2. Krawędź graniastosłupa łączy dwa z nich.
3. Sześcian, to szczególny przypadek tej bryły.
4. Np. osiowa, środkowa.
5. Całkowita – parzysta, albo nieparzysta.
6. Dział matematyki zajmujący się własnościami figur płaskich.
7. Powstaje w wyniku obrotu prostokąta wokół jednego z boków.
8. Dzieli kąt na połowy.
9. Aby go wykazać dla trójkątów prostokątnych, wystarcza równość pary kątów ostrych.
10. Jest wspólny podczas dodawania ułamków.
11. Część prostej zawierająca dwa punkty i wszystkie punkty między nimi.
12. Może pozostać w wyniku dzielenia liczb całkowitych.
13. Zawiera co najmniej jedną niewiadomą.
14. Jedna setna część kilometra kwadratowego.
15. Kąty o równych miarach, wyznaczone przez dwie proste przecinające się.
16 Uzasadnia prawdziwość twierdzenia.
17. Czworokąt posiadający co najmniej jedną parę boków równoległych.
18. Dla zdarzenia pewnego wynosi 1.
19. Element dziedziny funkcji.
20. Dla liczb 5, 6, 10 wynosi 7 (dwa słowa).
W pudełku znajduje się 60 losów. Prawdopodobieństwo wyciągnięcia losu wygrywającego wynosi \(\frac{1}{5}\). Bartek wyciągnął jeden los, który okazał się losem przegrywającym. Wyciągnięty los nie został zwrócony do pudełka.
- Przed losowaniem Bartka losów przegrywających było 5 razy więcej niż wygrywających. PRAWDA/FAŁSZ
- Prawdopodobieństwo, że losująca po Bartku Ania także wyciągnie los przegrywający, jest większe niż było u Bartka.PRAWDA/FAŁSZ
- Prawdopodobieństwo, że losująca po Bartku Ania wyciągnie los wygrywający, wynosi \(\frac{12}{59}\). PRAWDA/FAŁSZ
Na Wielkiej Skoczni rozegrano mistrzostwa w skokach narciarskich. Skok Gregora na odległość 148,5 m był o 12,5% dłuższy od skoku Kamila. Kamil skoczył o 10% dalej niż Tomek. Jeżeli długość skoku Tomka oznaczymy przez „x”, to długość skoku
- Kamila jest równa x +10%. PRAWDA/FAŁSZ
- Tomka można wyliczyć z równania 1,1×1,125x = 148,5. PRAWDA/FAŁSZ
- Gregora można opisać wyrażeniem (x +10%x)+12,5%× (x +10%x). PRAWDA/FAŁSZ
- \(\left( \sqrt[3]{3}-1 \right)\cdot \left( \sqrt[3]{9}+\sqrt[3]{3}+1 \right)=2\) PRAWDA/FAŁSZ
- \(\sqrt{2,5}\cdot \sqrt[3]{0,1}\cdot \sqrt{10}\cdot \sqrt[3]{1,25}=1\) PRAWDA/FAŁSZ
- \(\left( \sqrt[3]{-2}+\sqrt{2} \right)\cdot \left( \sqrt[3]{-2}-\sqrt{2} \right)=2\) PRAWDA/FAŁSZ
Liczbę a utworzono, zapisując kolejno liczby naturalne od 1 do 2013.
- Na setnym miejscu w zapisie liczby a jest cyfra 5. PRAWDA/FAŁSZ
- Liczba a składa się 6945 cyfr. PRAWDA/FAŁSZ
- Liczba a jest większa od \({{10}^{7000}}\). PRAWDA/FAŁSZ
- Jeżeli z doby pozostało jeszcze \(\frac{2}{3}\) tego co upłynęło, to wtedy jest godzina 14:24. PRAWDA/FAŁSZ
- Jeżeli z doby upłynęło 2 razy więcej czasu, niż jeszcze pozostało, to wtedy jest godzina 15:00. PRAWDA/FAŁSZ
- Jeżeli 2 godziny temu upłynęło o 1 godzinę więcej doby, niż zostało, to wówczas jest godzina 14:30. PRAWDA/FAŁSZ
Wykonanie dzielenia z resztą może być sposobem na obliczenie,
- w którym dniu tygodnia przypadnie powrót do pracy z urlopu trwającego 15 dni i rozpoczynającego się w poniedziałek. PRAWDA/FAŁSZ
- o której godzinie zakończyła się trwająca 70 godzin próba pobicia pewnego rekordu rozpoczęta o godzinie 12 w południe. PRAWDA/FAŁSZ
- którego dnia miesiąca upłynie 30-dniowy termin wykonania zalecenia kontrolnego, wydanego 5 dnia pewnego miesiąca. PRAWDA/FAŁSZ
Figurę złożoną z dwóch stożków można otrzymać w wyniku obrotu
- rombu dookoła jednej z jego przekątnych. PRAWDA/FAŁSZ
- trójkąta prostokątnego dookoła przeciwprostokątnej. PRAWDA/FAŁSZ
- trapezu wokół krótszej podstawy. PRAWDA/FAŁSZ
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
W punkcie usługowym jednostronne kopiowanie kartki kosztuje 7 gr, a dwustronne – 12 gr. Za odbicie 40 kartek, wśród których znajdowały się kartki kopiowane jednostronnie i kartki kopiowane dwustronnie, Janek zapłacił 3,45 zł. Ile kosztowałyby odbitki, gdyby każdą stronę kopiowano na osobnej kartce?
Treść dostępna po opłaceniu abonamentu.Udowodnij, że jeżeli liczba całkowita m przy dzieleniu przez 7 daje resztę 4, a liczba całkowita n przy dzieleniu przez 7 daje resztę 3, to iloczyn mn przy dzieleniu przez 7 daje resztę 5.
Treść dostępna po opłaceniu abonamentu.W pewnej firmie średnia arytmetyczna miesięcznych zarobków wszystkich pracowników wynosi 2328 zł. Rozkład tych zarobków przedstawiono w tabeli.
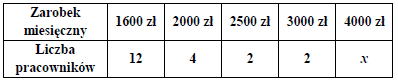
Ustal, która wartość jest większa: mediana czy średnia arytmetyczna miesięcznych zarobków pracowników tej firmy. Odpowiedź uzasadnij.
Treść dostępna po opłaceniu abonamentu.Wykresy funkcji: y = x + 2; y = x – 2; y = -x + 2; y = -x – 2 wyznaczają kwadrat ABCD. Znajdź wzory funkcji, których wykresy wyznaczają kwadrat A’B’C’D’ podobny do kwadratu ABCD w skali k = 3 i taki, że wierzchołki kwadratu A’B’C’D’ są punktami osi układu współrzędnych. Uzasadnij odpowiedź.
Treść dostępna po opłaceniu abonamentu.Przedstawiona na rysunku bryła CDIJGH, jest częścią sześcianu o krawędzi a taką, że czworokąt IJGH jest prostokątem, natomiast \(\left| \angle CGJ \right|=\left| \angle DHI \right|=30{}^\circ \). Oblicz objętość i pole powierzchni całkowitej tej bryły.
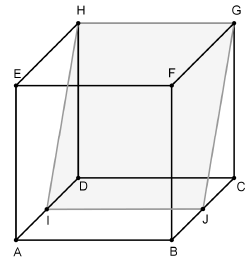 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.