Konkurs kuratoryjny z matematyki 2012/13 – Śląskie – Etap szkolny
Poniżej znajdują się zadania etapu szkolnego matematycznego konkursu kuratoryjnego z województwa śląskiego z roku 2012-2013 wraz z rozwiązaniami.
Rozwiąż krzyżówkę. Hasło, którym jest imię greckiego matematyka, odczytasz w zacieniowanych okienkach. Nie jest ono oceniane, ale zweryfikuje Twoje odpowiedzi.
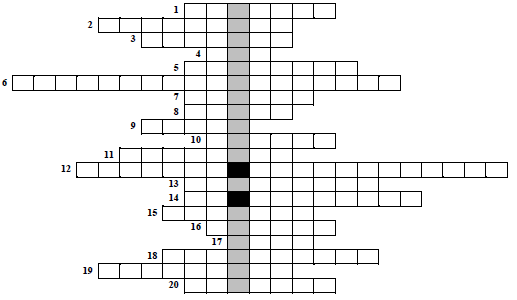
1. Prosta przecinająca okrąg w dwóch punktach.
2. Zasłynął z twierdzenia o trójkącie prostokątnym.
3. Wartość środkowa danych ułożonych niemalejąco.
4. Słownie: XL + LX.
5. Kąt, którego miara jest dwa razy większa niż miara kąta wpisanego opartego na tym samym łuku to kąt …
6. Najdłuższy bok w trójkącie prostokątnym.
7. Kwadrat ma … osie symetrii.
8. Powierzchnia kuli.
9. Wartość wyrażenia \({{\left( a+b\sqrt{3} \right)}^{0}}\) słownie.
10. 100 arów.
11. Liczba, której dzielnikami są tylko jeden i ona sama.
12. Suma n liczb podzielona przez n.
13. Odcinek łączący dwa niekolejne wierzchołki wielokąta.
14. Geometryczna interpretacja zbioru liczb rzeczywistych.
15. Dziesięć razy więcej niż promil z danej wartości.
16. Graficzne przedstawienie funkcji w układzie współrzędnych.
17 Czworokąt, którego przekątne dzielą się na połowy pod kątem prostym.
18 Punkt przecięcia tych prostych wyznacza środek okręgu opisanego na trójkącie.
19 W potędze \({{a}^{n}}\) jest nim n.
20 Prosta mająca dokładnie jeden punkt wspólny z okręgiem.
W figurze przedstawionej na rysunku można wyróżnić
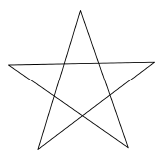
- 5 trójkątów rozwartokątnych. PRAWDA/FAŁSZ
- 10 trójkątów ostrokątnych. PRAWDA/FAŁSZ
- 10 trójkątów równoramiennych. PRAWDA/FAŁSZ
W trójkącie prostokątnym krótsza przyprostokątna ma długość a. Druga przyprostokątna jest 6 razy dłuższa od niej.
- Obwód tego trójkąta jest równy \(7a+\sqrt{37}a.\) PRAWDA/FAŁSZ
- Pole tego trójkąta wynosi \(\frac{7}{2}{{a}^{2}}.\) PRAWDA/FAŁSZ
- Jedna z wysokości tego trójkąta ma długość a. PRAWDA/FAŁSZ
Punkty: A, B, C, D, E, F, G, H, w podanej kolejności, podzieliły okrąg o środku O na osiem równych łuków.
- Miara kąta AEC wynosi \(45{}^\circ \) . PRAWDA/FAŁSZ
- Miara kąta HEB wynosi \(30{}^\circ \) . PRAWDA/FAŁSZ
- Miara kąta DOB jest taka sama jak miara kąta GEC. PRAWDA/FAŁSZ
- Odcinek ma tylko jedną oś symetrii. PRAWDA/FAŁSZ
- Prosta ma dokładnie jedną oś symetrii. PRAWDA/FAŁSZ
- Prosta ma nieskończenie wiele środków symetrii. PRAWDA/FAŁSZ
Jeżeli każdej liczbie dwucyfrowej przyporządkuje się iloczyn jej cyfr, to
- największą przyporządkowaną liczbą jest 99. PRAWDA/FAŁSZ
- najmniejszą przyporządkowaną liczbą jest 0. PRAWDA/FAŁSZ
- liczbom 16 i 32 przyporządkowana jest taka sama wartość. PRAWDA/FAŁSZ
Na miesięczną pensję sprzedawcy składa się stała kwota 1 000 zł i 5% wartości sprzedanego towaru.
- Wartość wynagrodzenia w wyraża wzór: w = 1000 + 0,5x , gdzie x oznacza wartość sprzedanego towaru. PRAWDA/FAŁSZ
- Aby zarobić nie mniej niż 2 000 zł, sprzedawca powinien sprzedać towar za co najmniej 20 000 zł. PRAWDA/FAŁSZ
- W miesiącu, w którym sprzedano towar za 18 000 zł, pensja sprzedawcy wynosiła 1 800 zł. PRAWDA/FAŁSZ
Przy drodze co 15 metrów rosną drzewa. Pasażer jadący samochodem policzył w ciągu 1 minuty 70 drzew.
- Samochód przejechał w ciągu minuty 1065 m. PRAWDA/FAŁSZ
- Średnia prędkość samochodu na tym odcinku miała wartość większą od 60 km/h. PRAWDA/FAŁSZ
- W ciągu 2 minut piechur idący ze stałą prędkością \(4,5\frac{km}{h}\) przejdzie obok co najmniej dziesięciu drzew. PRAWDA/FAŁSZ
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Równanie: \(C=\frac{5}{9}F-\frac{160}{9}\) – ustala zależność między temperaturą wyrażoną w stopniach Celsjusza (C) oraz Fahrenheita (F).
- Woda, w warunkach normalnych, wrze w temperaturze \(200{}^\circ F\). PRAWDA/FAŁSZ
- Woda, w warunkach normalnych, zamarza w temperaturze \(32{}^\circ F\). PRAWDA/FAŁSZ
- Zależność między temperaturą w stopniach Fahrenheita (F) a temperaturą w stopniach Celsjusza wyraża wzór: \(F=\frac{9}{5}C+32.\) PRAWDA/FAŁSZ
Według legendy na płycie nagrobnej greckiego matematyka Diofantosa był taki napis ułożony przez Euhopiusa:
Przechodniu. Pod tym kamieniem spoczywają prochy Diofantosa, który umarł w późnej starości. Przez szóstą część swego życia był dzieckiem, przez dwunastą część – młodzieńcem. Następnie upłynęła siódma część jego życia, zanim się ożenił. W pięć lat po zawarciu związku małżeńskiego narodził mu się syn, który żył dwa razy krócej od niego. W cztery lata po śmierci swego syna, opłakiwany przez swych najbliższych, zasnął snem wiecznym. Oblicz, ile lat żył Diofantos?
Wykaż, że przekątne równoległoboku dzielą się na połowy.
Treść dostępna po opłaceniu abonamentu.W trójkąt równoboczny ABC o boku 10 cm wpisano kwadrat KLMN, tak jak na rysunku. Oblicz pole tego kwadratu.
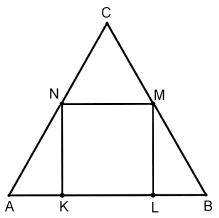 Treść dostępna po opłaceniu abonamentu.
Treść dostępna po opłaceniu abonamentu.
Ustal, czy liczba \({{123}^{123}}+{{67}^{67}}\) jest podzielna przez 10. Odpowiedź uzasadnij.
Treść dostępna po opłaceniu abonamentu.



