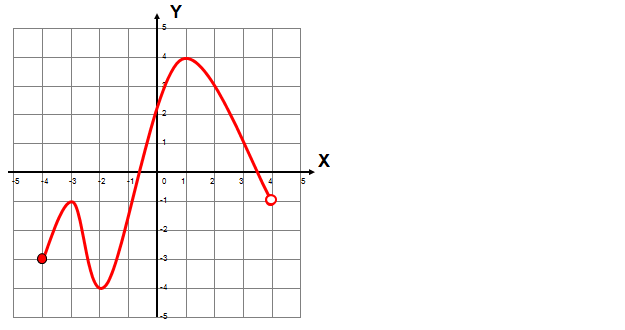Dziedzina i zbiór wartości funkcji
Dziedzina funkcji – to zbiór argumentów funkcji, czyli zbiór wszystkich x-ów należących do tej funkcji. W praktyce są to wszystkie liczby, które możemy wpisać do wzoru funkcji. Dziedzinę funkcji możemy również odczytać z wykresu. Wówczas patrzysz w jakiej części osi X leżą punkty Twojego wykresu.
Dziedzinę funkcji najczęściej oznaczamy przez: X, D, Df.
Zbiór wartości funkcji – jest to zbiór wszystkich y-ów należących do tej funkcji. Są to liczby, które możemy wyznaczyć wstawiając poszczególne argumenty „x” do wzoru funkcji. Bardzo często też można spotkać zadania, w których należy odczytać zbiór wartości z wykresu funkcji. W takiej sytuacji patrzysz w jakiej części osi Y leży wykres funkcji.
Zbiór wartości najczęściej oznaczamy przez: Y lub ZW.
Dla osób, które mają problem z wyznaczaniem dziedziny z wykresu proponuję narysować wykres w układzie współrzędnych ołówkiem lub kredą. Następnie wyznaczając dziedzinę funkcji zetrzyj całą pionową oś Y. Teraz zastanawiasz się w jakiej części osi X występuje wykres funkcji. Zbiór x-ów stanowi dziedzinę funkcji odczytanej z wykresu funkcji.
Ze zbiorem wartości postępujemy podobnie. Narysuj wykres funkcji, dalej zetrzyj oś poziomą X. Teraz odpowiedz w jakiej części osi pionowej Y znajduje się wykres Twojej funkcji. Zbiór y-ów jaki otrzymałeś jest Twoim zbiorem wartości funkcji.
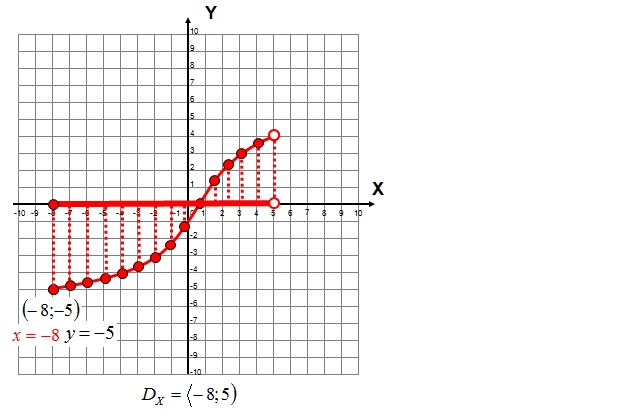
Określ dziedzinę i zbiór wartości funkcji na podstawie wykresu:
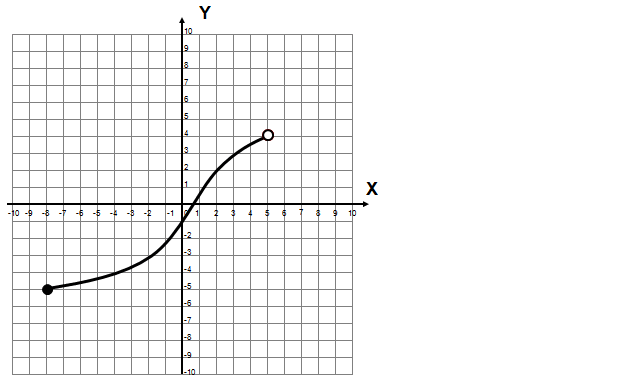
Rozwiązanie: wyznaczenie dziedziny funkcji.
Warunki pomagające wyznaczyć dziedzinę ze wzoru funkcji
- mianownik nie może być zerem
- wyrażenie podpierwiastkowe nie może być ujemne
W zasadzie większość zadań opartych na wyznaczaniu dziedziny ze wzoru oparta jest na tych dwóch warunkach. Zmieniają się tylko funkcje występujące w mianowniku lub pod pierwiastkiem.
Zobacz już teraz ciekawe zadania online dotyczące wyznaczania zbioru argumentów i wartości funkcji. W razie jakichkolwiek problemów z rozwiązaniem zadania, skorzystaj z gotowych rozwiązań wideo zamieszczonych poniżej.
Dziedzina i zbiór wartości funkcji na podstawie wykresu
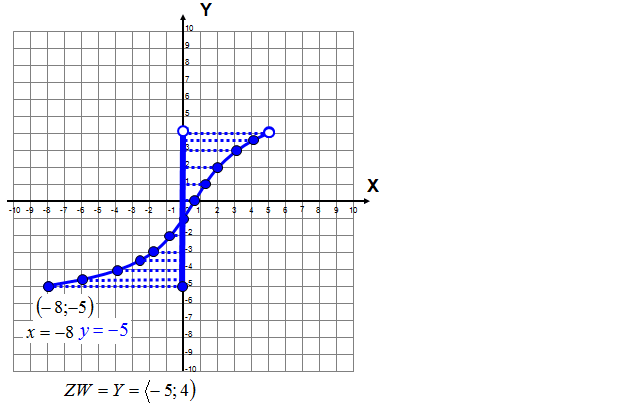
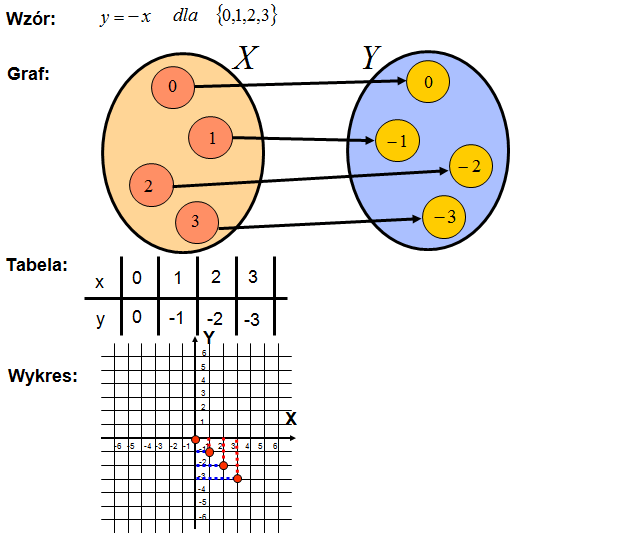
Mając opis słowny funkcji: „każdej liczbie naturalnej mniejszej lub równej 3 przyporządkowujemy liczbę przeciwną” wyznacz: dziedzinę i zbiór wartości funkcji.
- Ucz się matematyki już od 25 zł. Instrukcja premium
- Uzyskaj dostęp do całej strony MatFiz24.pl
- Wesprzyj rozwój filmów matematycznych
Zbiór argumentów – zbiór x-ów to dziedzina funkcji. We wszystkich wyżej wymienionych przykładach dziedzinę wyznaczasz wypisując cały zbiór x-ów.
Określ dziedzinę i zbiór wartości funkcji na podstawie wykresu funkcji stałej:
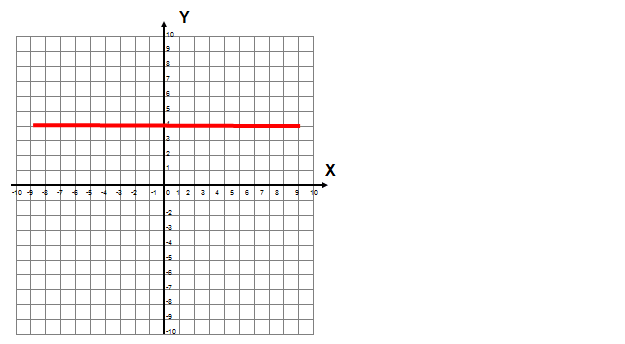
Rozwiązanie – dziedzina funkcji stałej:
Treść dostępna po opłaceniu abonamentu.Funkcja stała jest określona w całym zbiorze liczb rzeczywistych, zatem dziedziną jest właśnie zbiór liczb rzeczywistych.
Rozwiązanie – zbiór wartości funkcji stałej:
Treść dostępna po opłaceniu abonamentu.Wyznaczając zbiór wartości funkcji stałej zauważamy, że mamy tylko jedną wartość. Tutaj wartość funkcji jest jednoelementowym zbiorem y∈{4}.
Wyznacz na podstawie wykresu dziedzinę funkcji kwadratowej: y=x2.
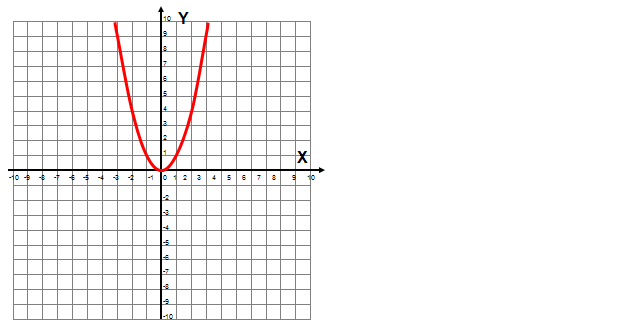
Rozwiązanie – dziedzina funkcji kwadratowej:
Treść dostępna po opłaceniu abonamentu.Rozwiązanie – zbiór wartości funkcji kwadratowej:
Treść dostępna po opłaceniu abonamentu.Rozwiązanie – zbiór wartości funkcji:
Treść dostępna po opłaceniu abonamentu.Rysunek przedstawia wykres funkcji f(x).
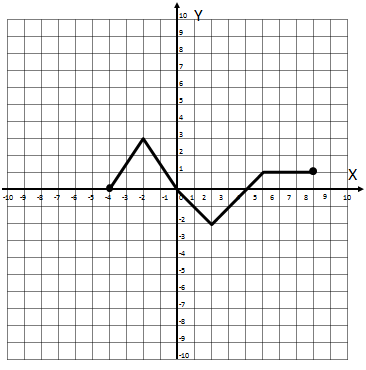
- Dziedziną funkcji f(x) są wszystkie liczby mniejsze od 8 i większe od –4. PRAWDA/FAŁSZ
- Funkcja f(x) ma dwa miejsca zerowe . PRAWDA/FAŁSZ
- Funkcja f(x) przyjmuje wartość równą 1 tylko dla argumentu 8. PRAWDA/FAŁSZ
Dziedzina i zbiór wartości funkcji na podstawie wzoru
Oblicz dziedzinę funkcji określonej wzorami: \(y=\frac{3}{x-5}\) oraz \( y=\frac{x}{6+x}\).
Rozwiązanie
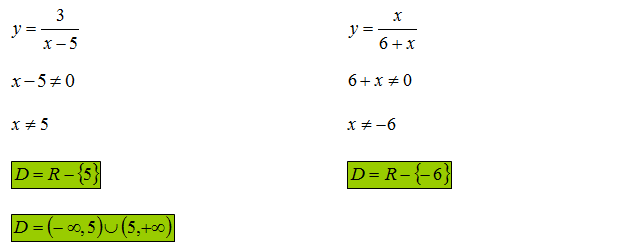
Podstawowym warunkiem na wyznaczanie dziedziny funkcji jest wykluczenie tych liczb, które zerują mianownik.
Oblicz dziedzinę funkcji określonej wzorami: \(y=\frac{x-1}{\left( x+2 \right)\ \left( x-3 \right)}\) oraz \( y = \frac{{5 – x}}{{x – 1}} – \frac{3}{{2 + x}}\).
Treść dostępna po opłaceniu abonamentu.Oblicz dziedzinę funkcji określonej wzorami: \(y = \frac{1}{{{x^2} – 1}}\) oraz \(y = \frac{{x + 3}}{{9 – {x^2}}}\)
Treść dostępna po opłaceniu abonamentu.Oblicz dziedzinę funkcji określonej wzorami: \(y = \frac{3}{{{x^2} + 2}}\) oraz \(y = \frac{{x – 2{x^2}}}{{3{x^4} – {x^3}}}\)
Treść dostępna po opłaceniu abonamentu.Oblicz dziedzinę funkcji określonej wzorami: \(y = \frac{{x + 17}}{{{x^2} – 4x + 4}}\) oraz \(y = \frac{{ – 3 – x}}{{{x^2} + 6x + 9}}\)
Treść dostępna po opłaceniu abonamentu.Wyznacz dziedzinę następujących funkcji: \(y = \frac{1}{{\left| {x – 2} \right| – 12}}\)
Treść dostępna po opłaceniu abonamentu.Wyznacz dziedzinę następującej funkcji: \(y = \frac{{x – 2}}{{\sqrt {{x^2} + 2x + 1} }}\)
Treść dostępna po opłaceniu abonamentu.Oblicz dziedzinę funkcji określonej wzorem: \(y = \sqrt {x + 5} \) oraz \(y = \sqrt {2 – 5x} \)
Treść dostępna po opłaceniu abonamentu.Oblicz dziedzinę funkcji określonej wzorem: \(y = \frac{{\sqrt {x – 2} }}{{\sqrt {8 – x} }}\)
Treść dostępna po opłaceniu abonamentu.Oblicz dziedzinę funkcji określonej wzorem: \(y = \sqrt {10 – \left| {5x + 2} \right|} \)
Treść dostępna po opłaceniu abonamentu.Oblicz dziedzinę funkcji określonej wzorem: \(y = \frac{1}{{x – 1}} + \sqrt {x + 2} \)
Treść dostępna po opłaceniu abonamentu.Oblicz dziedzinę funkcji określonej wzorem: \(y = \frac{{\sqrt {6 – x} }}{{{x^2} – 25}} + \frac{1}{{\sqrt {x – 1} }}\)
Treść dostępna po opłaceniu abonamentu.Oblicz dziedzinę funkcji określonej wzorem: \(y = \sqrt {14x + 49} + \frac{{x + 3}}{{\sqrt {x – 4} }}\)
Treść dostępna po opłaceniu abonamentu.